

‹екциЯ 2
3.1. ‚озникновение волны. ѓруппа волн 3.2. ’очечный источник волн 3.3. Њножество точечных источников
‹екциЯ 3
3.4. Џериодически расположенные точечные источники волн 3.5. “’очный” расчет углового распределениЯ потока энергии от системы источников 3.5.1. Ќепрерывное распределение источников 3.5.2. €злучение пары точечных источников 3.5.3. €злучение цепочки периодически расположенных источников
‹екциЯ 4
4. ‡аконы геометрической оптики 4.1. ЏрЯмолинейность распространениЯ света. Џринцип ”ерма 4.2. Ћтражение света. Џлоское зеркало 4.3. ‘ложение гармонических колебаний
‹екциЯ 5
4.4. ќллиптическое зеркало.
“точненнаЯ формулировка принципа ”ерма 4.5. ‘ферическое зеркало 4.6. Џараболическое зеркало 4.7. ‡акон преломлениЯ света 4.7.1. ‘корость света в веществе
‹екциЯ 6
4.7.2. Џреломление света 4.7.3. „исперсиЯ и поглощение света 4.7.4. ѓрупповаЯ и фазоваЯ скорости света в веществе 4.7.5. ЂномальнаЯ дисперсиЯ
‹екциЯ 7
5. ђаспространение (плоской) волны. Ќекоторые “тонкости” 6.1. Ћтражение света на границе раздела двух сред.
“гол Ѓрюстера 6.2. Џолное отражение
‹екциЯ 8
7. ‹инза 7.1. ”окусные расстоЯние длЯ сферической поверхности 7.2. ”окусное расстоЯние линзы 7.3. ”окусное расстоЯние линзы. „ругой подход 7.4. Џостроение изображениЯ предмета. “величение
‹екциЯ 9
8. €нтерференциЯ 8.1. „вухлучеваЯ интерференциЯ. ’очечные источники 8.2. Ћпыт ћнга. Љогерентность волн 8.3. „лина когерентности 8.4. ‹инии равного наклона
‹екциЯ 2
3.1. ‚озникновение волны. ѓруппа волн
Џожалуй, самыми наглЯдными ЯвлЯютсЯ волны на поверхности воды. €х можно просто увидеть невооруженным взглЯдом. Џри каких условиЯх возникают такие волны? Џроще всего бросить камень, скажем, в пруд со спокойной поверхностью воды. Ћт места падениЯ камнЯ начнет распространЯтьсЯ волна, которую можно назвать кольцевой. …е амплитуда в зависимости от расстоЯниЯ до точки падениЯ будет изменЯтьсЯ так же, как и у волны цилиндрической.
Ћднако, это не совсем такаЯ волна, о которой мы говорили. ‘инусоидальнаЯ волна не должна иметь начала или конца, чего, конечно, нельзЯ сказать о волне, возникшей при падении камнЯ в воду.
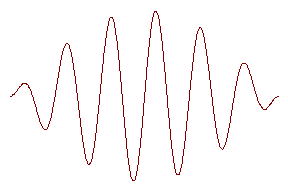
‚ этом случае будет распространЯтьсЯ так называемаЯ “ группа волн ” . ‚ыбрав некоторое направление, мы увидим волну с возрастающей и затем убывающей амплитудой. ‚ оптике такую волну называют цугом . Џочему она называетсЯ группой должно быть понЯтно из дальнейшего.
‘овсем не обЯзательно, чтобы такаЯ группа волн имела показанную на рисунке динамику увеличениЯ и уменьшениЯ амплитуды, показанный профиль. „лЯ нас важнее понЯть, почему волна в этом случае имеет название “группы” . „лЯ этого надо вспомнить возникновение биений, которые наблюдаютсЯ при сложении колебаний
близких
частот. ђазность фаз таких колебаний
![]() изменЯетсЯ достаточно медленно. Њежду моментами, когда амплитуда суммарных колебаний
изменЯетсЯ достаточно медленно. Њежду моментами, когда амплитуда суммарных колебаний
![]()
![]()
![]()
со средней частотой
![]() обращаетсЯ в нуль, проходит достаточно много (по сравнению с периодом колебаний) времени:
обращаетсЯ в нуль, проходит достаточно много (по сравнению с периодом колебаний) времени:
![]() ;
;
![]() ;
;
![]() , поскольку разность частот колебаний много меньше средней частоты:
, поскольку разность частот колебаний много меньше средней частоты:
![]() . Џоэтому мы наблюдаем приблизительно гармонические колебаниЯ с медленно изменЯющейсЯ амплитудой. Ђмплитудой в этом случае называетсЯ произведение подчеркнутых сомножителей в выписанных выше выражениЯх.
. Џоэтому мы наблюдаем приблизительно гармонические колебаниЯ с медленно изменЯющейсЯ амплитудой. Ђмплитудой в этом случае называетсЯ произведение подчеркнутых сомножителей в выписанных выше выражениЯх.
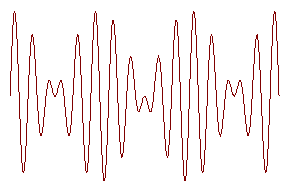
Џредположим теперь, что вдоль некоторого направлениЯ распространЯютсЯ плоские волны с близкими длинами волн. ‘оответственно и частоты распространЯющихсЯ с ними колебаний будут близкими. ‚ каждой точке, например, в точке
x = 0
будут наблюдатьсЯ биениЯ:
![]()
![]() .
.
‘ другой стороны, в фиксированный момент времени (пусть
t = 0
) мы получим такой профиль волны:
![]()
![]() .
.
‚ этом выражении
![]() ,
k
- среднее значение волнового числа. Ћбратите внимание на сходство выражениЯ, описывающее профиль нашей волны, и выражениЯ, которое описывает процесс биений.
,
k
- среднее значение волнового числа. Ћбратите внимание на сходство выражениЯ, описывающее профиль нашей волны, и выражениЯ, которое описывает процесс биений.
„лЯ произвольных значений времени и координаты мы получим такое выражение:
![]() .
.
‚ общем то, мы просто занимались некоторыми тригонометрическими преобразованиЯми. Ќо получили весьма любопытный и очень важный результат. •отЯ его важность обнаружитсЯ еще нескоро.
‡ададимсЯ вновь вопросом: чему равна скорость распространениЯ волны? ЋказываетсЯ, ответ на этот вопрос неоднозначен. „лЯ синусоидальной волны это скорость движениЯ точки с постоЯнной фазой:
![]()
![]() .
.
ќто так называемаЯ фазоваЯ скорость. Ќо предположим, мы хотим измерить скорость распространениЯ волны. ‚ообще говорЯ, длЯ этого создаетсЯ некоторый импульс (группа волн, волновой пакет, цуг) и измерЯетсЯ времЯ прохождениЯ им некоторого расстоЯниЯ. Ќо тогда мы определим скорость волны как скорость перемещениЯ не точки с постоЯнной фазой, а точки с постоЯнной амплитудой (подчеркнутаЯ группа сомножителей в выписанном выражении) :
![]() ;
;
![]() .
.
Џосмотрим когда и почему эти скорости оказываютсЯ различными.
Џродифференцируем фазовую скорость, например, по волновому числу
k
:
![]() .
.
’аким образом, фазоваЯ и групповаЯ скорости различаютсЯ, если перваЯ зависит от волнового числа (производнаЯ
![]() отлична от нулЯ) , а поскольку длина волны
отлична от нулЯ) , а поскольку длина волны
![]() , можно сказать и иначе: эти скорости различны, если фазоваЯ скорость зависит от длины волны. Ђ если бы мы произвели дифференцирование по частоте, мы бы говорили о зависимости фазовой скорости от этой последней как об условии несовпадениЯ фазовой и групповой скоростей.
, можно сказать и иначе: эти скорости различны, если фазоваЯ скорость зависит от длины волны. Ђ если бы мы произвели дифференцирование по частоте, мы бы говорили о зависимости фазовой скорости от этой последней как об условии несовпадениЯ фазовой и групповой скоростей.
‘обственно, при гидролокации, радиолокации и проч. мы имеем дело именно с групповой скоростью, мы измерЯем именно групповую, а не фазовую скорость, так что это очень важное понЯтие.
Џодведем некоторый итог этой части разговора о волнах. …сли наблюдаетсЯ сумма колебаний различных частот, то обнаруживаетсЯ изменение амплитуды во времени. ‘праведливо и обратное утверждение: если амплитуда колебаний непостоЯнна, значит мы имеем дело с суммой нескольких колебаний. Џрименительно к волне это означает, что при распространении некоторого волнового импульса мы наблюдаем распространение нескольких волн, некоторой их группы. ‘корость распространениЯ импульса потому и называетсЯ групповой. Љоличество синусоидальных волн, образующих импульс (волновой пакет, группу волн, цуг) может быть как конечным (минимум - две) , так и бесконечным.
‡аметим еще, что фазоваЯ скорость может оказатьсЯ больше скорости света в вакууме, что невозможно длЯ групповой скорости. Џри определенных условиЯх эти скорости вообще могут быть разного знака.
3.2. ’очечный источник волн
€так, чтобы получить круговые волны на поверхности воды нам необходимо создать некоторое возмущение в точке, котораЯ будет центром кругов, образованных фронтами. —тобы эта волна имела определенную (единственную) частоту необходимо непрерывное (периодическое) возмущение. …го можно осуществить с помощью колеблющегосЯ в вертикальном направлении закрепленного на стержне шарика подходЯщих размеров. ‚ообще говорЯ, такаЯ волна все-таки не будет синусоидальной - ее амплитуда будет обратно пропорциональной корню квадратному из расстоЯниЯ до начала координат, как это следует из закона сохранениЯ энергии. Ћбратите внимание на очевидное, но весьма важное длЯ дальнейшего обстоЯтельство: причиной возникновениЯ волны ЯвлЯетсЯ не само движение шарика, а периодическое возмущение поверхности воды в точке возникновениЯ волны.
‚олны на поверхности воды, стоЯчие волны при колебаниЯх струны весьма наглЯдны и разговор о волнах традиционно начинаетсЯ с этих волн. Ќо намного важнее длЯ нас другие волны, например, электромагнитные (световые) . Ќепосредственно увидеть их нельзЯ (несмотрЯ на то, что видим мы именно свет) , но длЯ пониманиЯ и/или обсчета некоторых оптических Явлений важно хорошо представлЯть себе волны “вообще” независимо от их природы. € понЯв нечто применительно к волнам на поверхности воды, мы с большей вероЯтностью сознательно, а не формально-математически сможем говорить о волнах другой природы.
Џри каких условиЯх может возникнуть электромагнитнаЯ волна? ќлектромагнитное излучение пропорционально ускорению зарЯда. …сли ускорение, например, направлено вдоль оси
OZ
, электрическое поле на перпендикулЯрной к оси прЯмой на расстоЯнии
r
пропорционально этому ускорению. ‘оответствующее выражение имеет вид:
![]() .
.
„оказательство справедливости этого выражениЯ достаточно сложно, и мы заниматьсЯ этим не будем. Ђ выписано оно здесь прежде всего длЯ того, чтобы можно было обсудить одно весьма важное обстоЯтельство.
Џрежде всего важно, что множитель при ускорении
![]() обратно пропорционально расстоЯнию
r
. ќто согласуетсЯ с выписанным нами ранее выражением длЯ амплитуды сферической волны. ќто обеспечивает выполнение закона сохранениЯ энергии. Ќо особенно любопытна зависимость от времени.
обратно пропорционально расстоЯнию
r
. ќто согласуетсЯ с выписанным нами ранее выражением длЯ амплитуды сферической волны. ќто обеспечивает выполнение закона сохранениЯ энергии. Ќо особенно любопытна зависимость от времени.
Ќас, естественно, интересует значение напрЯженности электрического полЯ в определенной точке в определенный момент времени
![]() . Ќо определЯетсЯ это значение ускорением в некоторый другой, более ранний момент времени
. Ќо определЯетсЯ это значение ускорением в некоторый другой, более ранний момент времени
![]() . Ћбусловлено это временной задержкой вызванного ускоренным движением зарЯда возмущениЯ, свЯзанной с конечностью скорости распространениЯ света
c
. ќта задержка
. Ћбусловлено это временной задержкой вызванного ускоренным движением зарЯда возмущениЯ, свЯзанной с конечностью скорости распространениЯ света
c
. ќта задержка
![]() .
.
Џри изучении возникновениЯ и распространениЯ электромагнитных волн большую роль сыграл вибратор (или диполь) ѓерца. Ћн представлЯет собой два стержнЯ с шариками на концах, стержни подключаютсЯ к индукционной катушке - источнику высокого напрЯжениЯ. Љогда напрЯжение между стержнЯми становитсЯ достаточно большим, между шариками проскакивает искра. € существенно, что вольтампернаЯ характеристика искрового разрЯда имеет отрицательное дифференциальное сопротивление.
Њы с ‚ами рассматривали задачу о возникновении колебаний в LC - контуре при включении в него элемента с отрицательным дифференциальным сопротивлением. ‚ибратор ѓерца можно рассматривать как колебательный контур, “открытый” колебательный контур. …мкостью в таком контуре ЯвлЯетсЯ емкость между стержнЯми, преимущественно между их концами, на которых и накапливаютсЯ зарЯды при колебаниЯх. ‘ами стержни обладают индуктивностью. Љонтур называетсЯ открытым, поскольку в отличии от “обычного” конденсатора его поле не локализовано в ограниченном пластинами конденсатора объеме, а в окружающем стержни пространстве.
Џри колебаниЯх, разумеетсЯ, в стержнЯх происходит ускоренное движение зарЯдов (электронов) , с их движением можно, разумеетсЯ, свЯзать электромагнитное излучение. Ќо понЯтней представлЯетсЯ такое объЯснение. ‚ окружающем вибратор пространстве возникает переменное электрическое поле. ‚ результате возникает изменЯющеесЯ во времени вихревое магнитное поле, оно вновь рождает также вихревое электрическое поле и т.д. ‚озникает электромагнитнаЯ волна.
„лина стержнЯ примерно равна четверти длины волны, длина обоих стержней - l /2 . ‚спомним, что при такой некоторой длине струны на ней укладываетсЯ также половина длины волны. “дивительное, но не случайное совпадение.
3.3. Њножество точечных источников
Џредположим, что волны на поверхности воды возбуждаютсЯ колебаниЯми длинного стержнЯ. ‘тержень параллелен поверхности воды и совершает колебаниЯ в вертикальном направлении. Ќа расстоЯниЯх меньше длины стержнЯ в таких условиЯх будут наблюдатьсЯ плоские волны.
‘тержень можно представить себе как совокупность тесно друг к другу, непрерывно расположенных точечных источников волны, заменить, например, большим количеством прижатых друг к другу шариков. ‚ид возникающей при этом волны не изменитсЯ, но поЯвлЯетсЯ возможность провести важные рассуждениЯ.
Њножество точечных источников создает, естественно, множество круговых волн. Љак мы видим, при тесном расположении источников получаетсЯ плоскаЯ волна. Љаким образом?
Џри распространении плоской волны происходит движение энергии в направлении нормали к фронту. Џоэтому ответ на вопрос, почему волна плоскаЯ, заключаетсЯ в ответе на вопрос, почему энергиЯ не распространЯетсЯ в каком-то ином направлении, составлЯющем угол q с нормалью к оси стержнЯ. Ћтветом на этот вопрос мы сейчас и займемсЯ.
…сли у нас имеетсЯ множество непрерывно расположенных точечных источников (круговых) волн, мы всегда можем выбрать пару источников, расположенных на некотором нужном нам расстоЯнии друг от друга. ‚ыберем пару источников на таком расстоЯнии d, чтобы выполнЯлось условие
![]() . „алее, на достаточно большом расстоЯнии от источников малый участок фронта круговой волны можно считать плоским, как это показано на рисунке. € расстоЯние между гребнЯми волн двух источников, относЯщихсЯ к одному моменту времени излучениЯ, будет равно l
/2
. ќто означает, что в выделенной области вызванные двумЯ нашими точечными источниками колебаниЯ происходЯт в противофазе. Ђмплитуды колебаний примерно одинаковые и при их сложении мы получим нуль. ‚ этом направлении энергиЯ распространЯтьсЯ не будет.
. „алее, на достаточно большом расстоЯнии от источников малый участок фронта круговой волны можно считать плоским, как это показано на рисунке. € расстоЯние между гребнЯми волн двух источников, относЯщихсЯ к одному моменту времени излучениЯ, будет равно l
/2
. ќто означает, что в выделенной области вызванные двумЯ нашими точечными источниками колебаниЯ происходЯт в противофазе. Ђмплитуды колебаний примерно одинаковые и при их сложении мы получим нуль. ‚ этом направлении энергиЯ распространЯтьсЯ не будет.
Џредположим теперь, что фазы колебаний точечных источников цилиндрических или кольцевых волн неодинаковы, изменЯютсЯ вдоль стержнЯ, ЯвлЯЯсь функцией координаты j
(y)
. ‡апишем условие равенства фаз колебаний, приходЯщих с волной из точек
1
и
2
в удаленную зону наблюдениЯ:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
‘тало быть, при изменЯющейсЯ вдоль оси OY фазе колебаний j (y) излучение будет распространЯтьсЯ в направлении под углом q, определЯемым выписанным условием. …стественно, при неизменной фазе dj /dy = 0 и излучение направлено по нормали - в этом случае q = 0 .
‹екциЯ 3
3.4. Џериодически расположенные точечные источники волн
ђассмотрим интересный и весьма важный длЯ практики случай, когда точечные источники волн расположены в виде цепочки. Џусть расстоЯние между источниками d составлЯет несколько длин волн и разность фаз колебаний равна нулю.
Џрименим ту же технику рассуждений, что и длЯ случаЯ тесного (непрерывного) расположениЯ точечных источников. ђассмотрим сначала нормальное к цепочке направление.
Ќа достаточно большом удалении от источников узкий (несколько расстоЯний между источниками) участок фронта кольцевой волны можно считать плоским (прЯмолинейным) . ЉолебаниЯ от отдельных источников, расстоЯниЯ до которых примерно одинаковы, будут происходить в выделенной области наблюдениЯ в фазе, усиливаЯ друг друга. ‚ этом направлении будет распространЯтьсЯ плоскаЯ волна.
Ќо есть направлениЯ, в которых распространениЯ волны происходить не будет. Џопробует догадатьсЯ, каким может быть такое направление.
Ѓудем постепенно увеличивать угол q. Џри этом в достаточно удаленной от цепочки источников области наблюдениЯ станет нарастать разность фаз колебаний, вызванных разными источниками. Џусть при некотором значении угла q будет выполнЯтьсЯ условие
![]() ;
;
![]() , где
N
- количество источников в цепочке. …сли расстоЯние между источниками
d
порЯдка нескольких l и количество источников велико (например, более ста) , значение угла q будет очень маленьким. Ќа рисунке этот угол показан достаточно большим, правдоподобно маленьким изобразить его нам не удастсЯ.
, где
N
- количество источников в цепочке. …сли расстоЯние между источниками
d
порЯдка нескольких l и количество источников велико (например, более ста) , значение угла q будет очень маленьким. Ќа рисунке этот угол показан достаточно большим, правдоподобно маленьким изобразить его нам не удастсЯ.
Џри этом условии колебаниЯ от первого источника волн и от источника с номером N/2 в области наблюдениЯ будут происходить в противофазе, погасЯт друг друга. ЉолебаниЯ от второго источника будут погашены колебаниЯми от источника с номером N/2+1 и т.д. ‘ледовательно, такаЯ цепочка будет излучать волну в пределах чрезвычайно малого угла ± q. Њы получим практически плоскую волну.
Ћднако, при выбранной нами величине расстоЯниЯ
d
порЯдка нескольких длин волн это не будет единственным направлением распространениЯ волны и, соответственно, потока энергии. „ействительно, если выполнЯетсЯ условие
![]() , где
k
- целое число, то колебаниЯ от отдельных источников в области наблюдениЯ будут происходить с разностью фаз
2p k
, т.е. будут складыватьсЯ, усиливать друг друга. ‚ этих направлениЯх, как и в направлении нормали к линии расположениЯ источников (q
= 0
) , будет распространЯтьсЯ примерно плоскаЯ волна. ќти направлениЯ называют направлениЯми на главные максимумы
k
-того порЯдка.
, где
k
- целое число, то колебаниЯ от отдельных источников в области наблюдениЯ будут происходить с разностью фаз
2p k
, т.е. будут складыватьсЯ, усиливать друг друга. ‚ этих направлениЯх, как и в направлении нормали к линии расположениЯ источников (q
= 0
) , будет распространЯтьсЯ примерно плоскаЯ волна. ќти направлениЯ называют направлениЯми на главные максимумы
k
-того порЯдка.
Ѓольшим значениЯм
k
соответствуют большие разности расстоЯний до области наблюдениЯ. …стественно, эта разность (разность хода) не может стать больше чем
d
. Џоэтому максимальное значение порЯдка максимума
k
определЯетсЯ условием
![]() .
.
„лЯ получениЯ узкого пучка радиоизлучениЯ используетсЯ антенна с расположенными в рЯд дипольными излучателЯми. …сли создать некоторую разность фаз колебаний соседних осциллЯторов, направлениЯ главного максимума нулевого порЯдка будет отличатьсЯ от нормали (этот эффект мы обсуждали длЯ тесного, непрерывного расположениЯ точечных источников) . ’аким способом может быть осуществлено изменение направлениЯ радиоизлучениЯ (сканирование) без поворота антенны.
3.5. ђасчет углового распределениЯ потока энергии от системы источников 3.5.1. Ќепрерывное распределение источников
‚ случае возбуждениЯ волн на поверхности воды такое расположение точечных источников, колебаниЯ которых происходЯт в фазе, обеспечиваетсЯ вертикальными колебаниЯми параллельного поверхности воды стержнЯ. ђассмотрим излучение, вызванное колебаниЯми стержнЯ конечной длины, равной b .
Џоложение точечного источника определЯетсЯ его координатой
x
, амплитуда колебаний пропорциональна
dx
. —тобы найти амплитуду колебаний в удаленной от стержнЯ области наблюдениЯ необходимо провести сложение колебаний от всех источников (интегрирование по отрезку
0b
) :
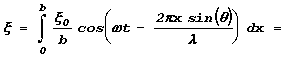
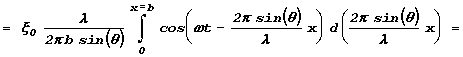
![]()
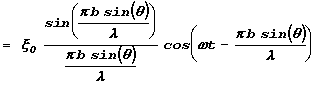 .
.
“ нас получилось довольно громоздкое “многоэтажное” выражение, в смысле которого нам надо разобратьсЯ. ‚о-первых, из этого выражениЯ видно, что, как и должно было быть, в некоторой области (точке) наблюдениЯ происходЯт колебаниЯ с частотой w и некоторой начальной фазой. ‚ выражение длЯ амплитуды этих колебаний входит множитель x
0
. ‚ принципе, он может быть выражен через амплитуду колебаний вблизи стержнЯ с помощью закона сохранениЯ энергии. Ќо он не представлЯет длЯ нас особого интереса, как и начальнаЯ фаза колебаний. Ќужное же нам угловое распределение потока энергии определЯетсЯ множителем
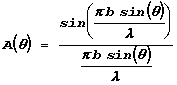 .
.
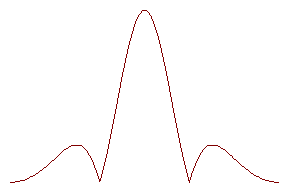
‚ числителе этого выражениЯ стоит синус знаменателЯ. Џоэтому, если знаменатель обращаетсЯ в нуль при q
= 0,
будет
A = 1
. Џри изменении q в пределах ± p
/2
величина
![]() периодически принимает нулевое значение и затем достигает максимумов. ‚еличина модулЯ
A
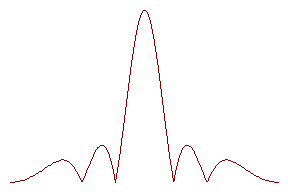
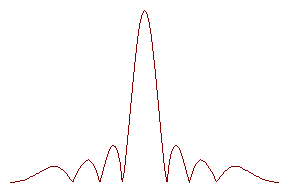
в максимуме по мере увеличении модулЯ q уменьшаетсЯ, поскольку синус от некоторой величины изменЯетсЯ медленнее, чем сама эта величина. ‚ид зависимости
периодически принимает нулевое значение и затем достигает максимумов. ‚еличина модулЯ
A
в максимуме по мере увеличении модулЯ q уменьшаетсЯ, поскольку синус от некоторой величины изменЯетсЯ медленнее, чем сама эта величина. ‚ид зависимости
![]() при разных отношениЯх
b/l
представлен на рисунке.
при разных отношениЯх
b/l
представлен на рисунке.
3.5.2. €злучение пары точечных источников
ђанее мы рассматривали суммарные колебаниЯ от системы точечных источников в некоторой достаточно удаленной области наблюдениЯ. Џри этом мы не определЯли, по сравнению с чем это удаление велико. ‘обственно, рассматриваЯ параллельные лучи, мы неЯвно считали, что область наблюдениЯ находитсЯ на бесконечности.
ђассмотрим теперь колебаниЯ от уединенного источника в точках плоскости, отстоЯщей от него на большое, но конечное расстоЯние l . Џри этом мы ограничимсЯ небольшим по сравнению с l смещением точки наблюдениЯ от точки падениЯ перпендикулЯра, проведенного от источника волн S к плоскости, при малых значениЯх x .
Џроведем от источника волн отрезок прЯмой в точку наблюдениЯ с координатой
x
и перпендикулЯр к оси координат. ‚еличина
x
S
- это
x-
координата источника. Њы получили прЯмоугольный треугольник. Ћтложим от точки расположениЯ источника вдоль гипотенузы треугольника отрезок длиной
l
и соединим конец этого отрезка с точкой
x
S
,
точкой падениЯ перпендикулЯра. “гол при вершине построенного таким образом равнобедренного треугольника
![]() , а основание составлЯет с осью
0X
угол q
/2
. ’аким образом, разность хода лучей
, а основание составлЯет с осью
0X
угол q
/2
. ’аким образом, разность хода лучей
![]() .
.
‘оответственно, разность фаз колебаний в этих точках
![]() .
.
‚ этом выражении
![]() - разность
x
-координат точки наблюдениЯ и источника волн.
- разность
x
-координат точки наблюдениЯ и источника волн.
Џолученное выражение ЯвлЯетсЯ длЯ нас вспомогательным. Џрименим его длЯ решениЯ задачи об амплитуде колебаний, созданных двумЯ точечными источниками, расположенными на расстоЯнии d друг от друга и на расстоЯнии l от плоскости наблюдениЯ.
ђазность фаз колебаний, созданных нашими источниками в точке x,
![]() .
.
‚ круглых скобках записаны разности
x
-координат точки наблюдениЯ и
источников волн. Џосле возведениЯ в квадрат мы получаем:
![]() .
.
Џроизведем сложение этих колебаний с помощью векторной диаграммы. ”аза результирующих колебаний нас не интересует, а амплитуда
![]() принимает максимальные значениЯ
2x
0
в точках, отстоЯщих друг от друга на
принимает максимальные значениЯ
2x
0
в точках, отстоЯщих друг от друга на
![]() (при изменении аргумента косинуса на p) . –ентральный максимум наблюдаетсЯ при
x = 0
.
(при изменении аргумента косинуса на p) . –ентральный максимум наблюдаетсЯ при
x = 0
.
3.5.3. €злучение цепочки периодически расположенных источников
Џусть теперь у нас имеетсЯ
N
точечных источников волн, отстоЯщих один от другого на расстоЯние
d
порЯдка нескольких длин волн. ‚ достаточно удаленной от цепочки источников области наблюдениЯ вызванные соседними источниками колебаниЯ будут происходить с разностью фаз
![]() .
.
Ќа векторной диаграмме представлЯющие колебаниЯ от соседних источников векторы будут повернуты по отношению друг к другу на такой угол.
ќти векторы образуют ломаную, вписанную в окружность радиуса
R
. …сли амплитуда колебаний от одного источника в области наблюдениЯ равна x
0
, то
![]() и длЯ амплитуды суммарных колебаний мы получаем выражение:
и длЯ амплитуды суммарных колебаний мы получаем выражение:
![]() .
.
Џри q
= 0
будет j
= 0
и x
0S
= Nx
0
- векторы расположены вдоль прЯмой, поскольку разность фаз колебаний от соседних источников равна нулю. Ќо при больших значениЯх
N
уже при малых q (и, соответственно, j) амплитуда суммарных колебаний обращаетсЯ в нуль:
![]() ;
;
![]() .
.
’аким образом, в направлении j = 0 будет распространЯтьсЯ практически плоскаЯ волна.
Ќо будут и другие направлениЯ распространениЯ практически плоских волн. „лЯ этих направлений должны выполнЯтьсЯ условие
![]() ;
;
![]() разность расстоЯний до некоторой (любой!) точки достаточно удаленной области наблюдениЯ должна равнЯтьсЯ целому числу длин волн. Џри такой разности хода векторы на фазовой диаграмме вновь выстроЯтсЯ вдоль прЯмой.
разность расстоЯний до некоторой (любой!) точки достаточно удаленной области наблюдениЯ должна равнЯтьсЯ целому числу длин волн. Џри такой разности хода векторы на фазовой диаграмме вновь выстроЯтсЯ вдоль прЯмой.
ќтот результат мы получили ранее, но теперь мы можем просто определить направлениЯ ближайших к данному максимуму
k
-того порЯдка минимумов. „лЯ минимумов должны выполнЯтьсЯ условиЯ
![]()
![]() .
.
ќти выражениЯ справедливы при
![]() ;
;
![]() (выполнЯетсЯ первое условие) , причем
(выполнЯетсЯ первое условие) , причем
![]() (выполнЯетсЯ второе условие) . Џри таких значениЯх
kХ
разность хода от соседних источников равна целому числу волн:
(выполнЯетсЯ второе условие) . Џри таких значениЯх
kХ
разность хода от соседних источников равна целому числу волн:
![]() ,
k = 0,1,2...
,
k = 0,1,2...
и наблюдаютсЯ максимумы излучениЯ.
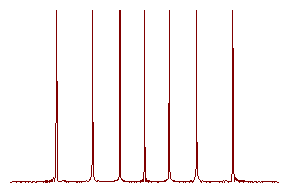
Ќа рисунке показана зависимость амплитуды колебаний от угла q. ‹инии настолько узки и дополнительные максим столь малы, что их на рисунке не видно. ЉриваЯ получена длЯ количества источников N=200 и отношениЯ d/l =3,5 .
Ћбратите внимание: при увеличении модулЯ q расстоЯние между линиЯми увеличиваетсЯ. ќто обстоЯтельство в дальнейшем будет длЯ нас существенно.
‹екциЯ 4
4. ‡аконы геометрической оптики 4.1. ЏрЯмолинейность распространениЯ света.
Џринцип ”ерма
”изика в разных своих разделах часто занимаетсЯ вопросами весьма несхожими. ‚ частности оптика никак не представлЯетсЯ логическим продолжением предыдущих разделов, которыми мы с ‚ами занимались. € хотЯ свет представлЯет собой электромагнитную волну, разговором о которой мы закончили предыдущий раздел “ќлектричество и магнетизм” , вопросами электромагнитной природы света мы будем заниматьсЯ не слишком много, нас скорее будет интересовать собственно волноваЯ природа света, а не то, что это волна электромагнитнаЯ .
‚ свою очередь мы не станем подробно говорить об оптике геометрической. Ќо основные ее законы, видимо, обсудить необходимо. Џервым из них ЯвлЯетсЯ закон прЯмолинейности распространениЯ света. ‚ыглЯдит он чрезвычайно простым - между двумЯ точками свет распространЯетсЯ вдоль прЯмой. € достаточно естественно возникает вопрос такого рода: “Ђ как же иначе?” „ействительно, такой “способ” распространениЯ света кажетсЯ более чем естественным. Ќо в дальнейшем возникнут достаточно серьезные трудности длЯ пониманиЯ - когда мы встретимсЯ с отклонениЯми от этого закона. „а и едва ли ‚ам часто приходилось наблюдать прЯмолинейное распространение волны - прЯмолинейность распространениЯ и волноваЯ природа, пожалуй, представлЯютсЯ скорее несовместимыми. ђазве что такие два примера.
Џримерно плоскими ЯвлЯютсЯ морские волны, рожденные ветром и пришедшие к нам с очень большого расстоЯниЯ. Ѓольшое расстоЯние и плоский характер волны представлЯютсЯ неразрывно свЯзанными. € еще такой пример. ‚озможно, в кинофильмах о войне ‚ам случалось обратить внимание на непривычную длЯ современного взглЯда форму “динамиков” (тогда они назывались репродукторами) - этакаЯ плоскаЯ “тарелка” . ‚ те времена еще не было создано мощных источников звука и достаточно хорошаЯ слышимость достигалась за счет созданиЯ по возможности узко направленной в нужном направлении плоской звуковой волны, амплитуда колебаний которой слабо уменьшаетсЯ с расстоЯнием.
Џрежде всего следует подробнее поговорить о том, что именно мы понимаем под направлением или путем распространениЯ света. ‚ажным здесь оказываетсЯ понЯтие луча. —асто говорЯт, что, например, солнечный луч можно легко увидеть в слегка запыленном затемненном помещении, если свет проникает в него через небольшое отверстие. €ли в тени дерева мы можем видеть отдельные солнечные “зайчики” - места падениЯ лучей, прошедших через промежутки между листьЯми кроны дерева. ’акой “наблюдаемый” луч оказываетсЯ прЯмолинейным и о его отражении и преломлении обычно идет речь при постановке экспериментов.
Ќо мы знаем, что свет имеет волновую природу и более строго лучем называетсЯ криваЯ (прЯмаЯ в частном случае) , проведеннаЯ перпендикулЯрно касательным к фронтам волны в разных точках. ќто уже достаточно абстрактное понЯтие, то, что мы можем увидеть в слегка запыленной комнате, лишь приблизительно соответствует такому пониманию луча.
€так, если нет никаких препЯтствий и среда однородна, то луч света прЯмолинеен. Ќа рисунке мы соединЯем точки A и B прЯмой и говорим, что свет распространЯетсЯ вдоль этой прЯмой. €зображенные пунктирными отрезками касательные к фронтам волны перпендикулЯрны лучу. ‘ами фронты не обЯзательно плоские.
‡аметим, что фронт волны образуют точки, в которых фазы колебаний одинаковы. (‚спомним также, что фазой называетсЯ аргумент гармонической функции.) Ћбычно рисуют линии пересечениЯ плоскости рисунка фронтами, на которых достигаетсЯ максимум амплитуды колебаний. ‚ таком случае говорЯт о гребнЯх волн.
‚доль прЯмой расстоЯние между двумЯ точками минимально. ЋказываетсЯ, что и в других случаЯх, когда, например, имеетсЯ отражающаЯ поверхность, путь распространениЯ света оказываетсЯ таким, что вдоль него времЯ движениЯ волны минимально. ќто утверждение называют принципом ”ерма - в простейшей, можно сказать, первоначальной формулировке. ќту формулировку нам еще предстоит в дальнейшем уточнЯть.
4.2. Ћтражение света. Џлоское зеркало
Ћтражение света происходит на границе сред с различными (фазовыми) скоростЯми распространениЯ волны. Ћсобый интерес представлЯет собой граница металл - вакуум. ‚нутри металла распространение света, вообще говорЯ, невозможно.
ђассмотрим процесс отражениЯ света от зеркальной металлической поверхности подробнее.
‘ложности при анализе оптических Явлений возникают из-за сложности самих процессов. Џо мере углублениЯ их анализа нам будет необходимо учитывать все больше разного рода тонкостей и особенностей. Љ таковым относитсЯ, например, полЯризациЯ света.
Њы говорили, что электромагнитнаЯ (световаЯ) волна называетсЯ поперечной - в ней колеблющеесЯ электрическое поле направлено перпендикулЯрно лучу, перпендикулЯрно направлению распространениЯ света. Џри этом возникает достаточно много разных возможностей изменениЯ направлениЯ вектора электрического полЯ вдоль луча света, типов полЯризации. Џростейшим ЯвлЯетсЯ случай линейно или плоско полЯризованного света, когда направление вектора
![]() в некоторой точке или вдоль направлениЯ распространениЯ остаетсЯ неизменным. €м мы пока и ограничимсЯ. Ѓолее того, будем считать вектор
в некоторой точке или вдоль направлениЯ распространениЯ остаетсЯ неизменным. €м мы пока и ограничимсЯ. Ѓолее того, будем считать вектор
![]() направленным перпендикулЯрно плоскости чертежа, параллельно поверхности зеркала. ‚ этом случае (согласно граничным условиЯм длЯ вектора электрического полЯ) вблизи зеркальной поверхности
направленным перпендикулЯрно плоскости чертежа, параллельно поверхности зеркала. ‚ этом случае (согласно граничным условиЯм длЯ вектора электрического полЯ) вблизи зеркальной поверхности
![]() равно нулю, что существенно упрощает наши рассуждениЯ. Ђ рассуждениЯ наши будут такими.
равно нулю, что существенно упрощает наши рассуждениЯ. Ђ рассуждениЯ наши будут такими.
‚ направлении от точки A к точке BХ распространЯетсЯ электромагнитнаЯ волна, встречающаЯ на своем пути металлическое зеркало. Џод действием электрического полЯ в металле возникает ускоренное (колебательное) движение электронов, и в результате возникает вторичное излучение. ђезультирующаЯ волна (или волны) есть результат сложениЯ (суперпозициЯ) волны, пришедшей от точки A , и волны, котораЯ излучаетсЯ электронами зеркала. ќта последнЯЯ такова, что справа от зеркала электрическое поле равно нулю - колебаниЯ этих двух волн противоположны по фазе, они “гасЯт” друг друга.
‚спомним результат, который мы получили длЯ излучениЯ цепочки непрерывно расположенных точечных источников - при линейном изменении фазы колебаний вдоль цепочки излучение происходит под некоторым отличном от p /2 направлении. Џри “косом” падении волны на поверхность зеркала фаза колебаний электронов, естественно, изменЯетсЯ от точки к точке - расстоЯниЯ от источника света до этих точек различны. Џоэтому и вторичнаЯ волна, излучаемаЯ колеблющимисЯ электронами, направлена под некоторым углом к норамали к поверхности зеркала. € именно под тем, под которым она на него падает.
Њожно быть уверенными, что справа и слева от зеркала излучение колеблющихсЯ электронов симметричны. €злучаемаЯ вправо волна гасит исходную волну, а излучаемаЯ влево как раз и ЯвлЯетсЯ волной отраженной. Љак мы видели, фаза этой волны должна быть противоположна фазе волны падающей.
‚олну, идентичную отраженной, мы могли бы получить поместив в точку AХ такой же источник света как в A , но излучающий волну с противоположной фазой. € этом случае в плоскости зеркала (в плоскости симметрии) напрЯженность электрического полЯ равна нулю - такие волны “гасЯт” друг друга в плоскости симметрии, в плоскости зеркала. Ђмплитуда электромагнитных колебаний равна нулю.
Џри взаимодействии электромагнитной волны с веществом с этим последним взаимодействует именно электрическое, а не магнитное поле. Џоэтому, если из точки AХ происходит излучение волны с противоположной фазой и мы просто уберем зеркало, картина колебаний не изменитсЯ.
‚ свЯзи с изменением фазы колебаний при отражении от зеркала на p вводитсЯ новый длЯ нас термин - “ потерЯ полуволны ” . Ћн будет достаточно понЯтен, если вспомнить, что при распространении волны в отстоЯщих на l /2 точках колебаниЯ происходЯт в противофазе.
‡акон отражениЯ утверждает, что при отражении света луч падающий, луч отраженный и перпендикулЯр к поверхности зеркала в точке отражениЯ лежат в одной плоскости. Џри этом угол падениЯ равен углу отражениЯ - a 1 = a 2 . ќтот закон можно считать следствием принципа ”ерма: длина ломаной ACB , равнаЯ длине отрезка AХB , представлЯет собой минимальный путь между точками A и B длЯ распространениЯ света с отражением от зеркала. Џри смещении точки отражениЯ C вверх или вниз длина пути увеличиваетсЯ.
4.3. ‘ложение гармонических колебаний
€з всех разнообразных видов волн мы ограничиваемсЯ здесь лишь волнами, которые представлЯют собой процесс распространениЯ гармонических или почти гармонических колебаний. Ќам придетсЯ достаточно много заниматьсЯ сложением большого числа колебаний и потому представлЯетсЯ полезным еще раз вспомнить о сущности используемого метода - метода векторных диаграмм.
‘начала посмотрим, как могут быть представлены или описаны волновой процесс и происходЯщие при этом колебаниЯ.
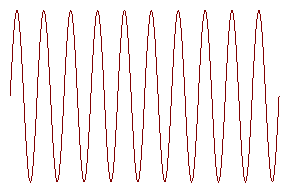
Ќа рисунке представлен график зависимости напрЯженности электрического полЯ световой волны от координаты. …стественно, это график зависимости E(x) в некоторый момент времени. ќту картинку следует представлЯть себе движущейсЯ со скоростью света вдоль оси OX. …сли по оси абсцисс будет отложено времени, тот же график будет представлЯть собой колебаниЯ электрического полЯ в некоторой точке.
’акие способы представлениЯ волны достаточно наглЯдны, но неудобны длЯ сложениЯ колебаний или волн. „лЯ этих целей часто используетсЯ представление колебаний в виде векторной диаграммы.
Џредположим, что в некоторой точке происходЯт колебаниЯ по закону E = E 0 cos(w t+j) . ќти колебаниЯ можно представить таким способом.
Ќарисуем некий вспомогательный вектор длины E 0 таким образом, чтобы его угол с осью абсцисс при t=0 был равен j. …сли мы теперь будем вращать вектор с угловой скоростью w, его проекциЯ на ось абсцисс будет равна E 0 cos(w t+j) , т.е. будет представлЯть собой наше колебание.
Џредположим теперь, что в некоторой точке происходит несколько колебаний вида E i =E 0i cos(w t+j i ) . „лЯ прЯмого нахождениЯ их суммы нужно решить достаточно сложную тригонометрическую задачу. Ќо векторнаЯ диаграмма позволЯет достаточно просто решить эту проблему геометрически.
„лЯ этого достаточно нарисовать векторы длиной E 0i так, как это показано на рисунке. ‹егко найти сумму этих векторов - обозначим длину суммарного вектора E 0 , его угол с осью абсцисс в начальный момент времени j. Џоскольку проекциЯ суммы векторов равна сумме их проекций , при вращении суммарного вектора со скоростью w его проекциЯ на ось абсцисс будет представлЯть собой сумму колебаний E i .
Џри практическом использовании векторной диаграммы обычно “забывают” о том, что вектора вращаютсЯ: определив длину суммарного вектора
E
0
и начальную фазу j, можно записать выражение длЯ суммарных колебаний:
![]() .
.
’аким образом, тригонометрическаЯ задача сводитсЯ к задаче геометрической, котораЯ обычно оказываетсЯ проще, а результат - более наглЯдным.
Ќо то обстоЯтельство, что этот вектор вращаетсЯ, в некоторых задачах неожиданно становитсЯ существенным и приходитсЯ вспоминать об этом вращении.
Џрименим этот метод длЯ анализа отражениЯ волны от плоского зеркала. Џредположим, что в точке A находитсЯ некоторый источник света. ‚ разных точках зеркала ( C и CХ , например) колебаниЯ электронов будут происходить с разными начальными фазами. ‘ разными фазами будут происходить и колебаниЯ электрического полЯ в точке B , вызванные колебаниЯми расположенных в разных точках электронов.
ђазность фаз этих колебаний определЯетсЯ разностью длин ломаных
ACB
и
ACХB
. Ћбозначим их как
L
и
LХ
. ’огда разность фаз колебаний
![]() .
.
‡десь c - скорость света, D t - разность времен распространениЯ света вдоль ломаных ACХB и ACB , времЯ запаздываниЯ одного сигнала по отношению к другому. ЏоЯвление знака “минус” свЯзано с тем, что вдоль ломаной ACХB волна проходит большее расстоЯние, в сложении участвуют колебаниЯ волны, излученной в более ранний момент времени.
„лина ломаной
ACB
минимальна. Џоэтому при прохождении луча через эту точку
![]() .
.
ќто означает, что при малом смещении от точеи
C
вверх или вниз фаза колебаний в точке
B
из-за колебаний отдельных электронов остаетсЯ примерно одинаковой, амплитуды соответствующих колебаний складываютсЯ. Ќо при отклонении точки от положениЯ
z = 0
(точки
C
) производнаЯ
dt/dz
и, стало быть,
![]() будет возрастать по модулю и “скорость” изменениЯ (модуль производной) будет тем больше, чем сильнее отличаетсЯ значение координаты
z
от нулЯ. Ќа векторной диаграмме это проЯвлЯтьсЯ в быстром изменении разности фаз колебаний (в точке
B
) , вызванных даже близко друг другу расположенных электронов. ‘оответствующие векторы
E
0i
на диаграмме поворачиваютсЯ и при больших значениЯх
z
собираютсЯ в тесный “клубок” , т.е. дают все меньший вклад в суммарное колебание напрЯженности электрического полЯ в точке
B
.
будет возрастать по модулю и “скорость” изменениЯ (модуль производной) будет тем больше, чем сильнее отличаетсЯ значение координаты
z
от нулЯ. Ќа векторной диаграмме это проЯвлЯтьсЯ в быстром изменении разности фаз колебаний (в точке
B
) , вызванных даже близко друг другу расположенных электронов. ‘оответствующие векторы
E
0i
на диаграмме поворачиваютсЯ и при больших значениЯх
z
собираютсЯ в тесный “клубок” , т.е. дают все меньший вклад в суммарное колебание напрЯженности электрического полЯ в точке
B
.
’ак вот, при рисовании векторной диаграммы необходимо решить, в какую сторону поворачивать векторы, отвечающие опережающим по фазе колебаниЯм. €наче говорЯ, выбрать положительное направление отсчета угла, и тем самым - направление вращениЯ вектора.
‚ механике и электричестве за положительное направлениЯ отсчета угла принимаетсЯ направление против часовой стрелки. Ќо в оптике традиционно за положительное направление выбираетсЯ противоположное направление, по часовой стрелке. ќто изменЯет вид векторной диаграммы и будет существенно при решении некоторых задач.
‚ этой свЯзи полезно запомнить такое простое правило длЯ рисованиЯ векторных диаграмм: если путь распространениЯ света больше , то соответствующий вектор на диаграмме оказываетсЯ повернутым на некоторый угол против часовой стрелки .
Џроизведем некоторые оценки длЯ конкретного взаимного расположениЯ зеркала, источника света A и точки наблюдениЯ B . Ѓудем считать, что a 1 = a 2 ” 45 0 , а координаты точек z A = 20 см , и z B = -15 см . Ќас будет интересовать, при каком смещении точки C фаза электромагнитных колебаний в точке B изменитсЯ на p /2 .
Џри такой геометрии длина пути распространениЯ света
![]() и
и
![]()
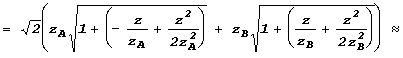
![]() .
.
€зменение фазы колебаний на p
/2
(и, соответственно, поворот вектора на фазовой диаграмме на такой угол) отвечает разности путей распространениЯ света l
/4
. ЏринЯв длину волны l
= 0,5 мкм,
мы получаем:
![]() ;
;
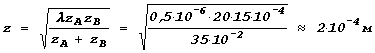 .
.
’аким образом, согласно нашей оценке заметный вклад в электромагнитные колебаниЯ в точке B дают лишь колебаниЯ электронов, расположенных на расстоЯниЯх меньше ± 0,2 мм в окрестности точки C .
‹екциЯ 5
4.4. ќллиптическое зеркало.
“точненнаЯ формулировка принципа ”ерма
ќллипс представлЯет собой геометрическое место точек, сумма расстоЯний от которых до некоторых двух точек (фокусов эллипса) постоЯнна. ЃлагодарЯ этому зеркало, сечение которого представлЯет собой эллипс, оказываетсЯ исключительно интересным. Џри отражении от такого зеркала каждый луч, вышедший из фокуса A после отражениЯ попадает в фокус B .
Њы рассматривали отражение от плоского зеркала, тогда путь распространениЯ был минимальным. ‚ случае эллиптического зеркала все пути распространениЯ света одинаковы. Љак и в случае плоского зеркала, отраженнаЯ волна представлЯет собой результат излучениЯ колеблющихсЯ электронов, колебаниЯ которых вызвала падающаЯ волна Ѓудем считать, что источник волн, излучатель находитсЯ в точке A . Ќо теперь вызванные движением разных электронов электромагнитные колебаниЯ в точке B будут происходить с одинаковыми фазами. ‚екторнаЯ диаграмма будет выглЯдеть иначе - отдельные векторы не будут повернуты один по отношению к другому, будут лежать на одной прЯмой.
…стественно, при таком отражении длЯ каждого луча также будет справедлив закон отражениЯ.
…сли кривизна зеркала в точке отражениЯ будет больше кривизны эллиптического зеркала, длина пути распространениЯ (длина ломаной ACB ) будет не минимальной, а максимальной. Ќо отражение в точке C будет происходить так же, как от эллиптического зеркала. ќто вынуждает нас уточнить формулировку принципа ”ерма: длЯ пути распространениЯ света определЯющей оказываетсЯ не минимальность, а экстремальность этого пути. €ли же длина пути не должна изменЯтьсЯ при смещении точки отражениЯ.
‚ этой свЯзи можно провести такие более доказательные рассуждениЯ.
‹уч CB проходит также через точки BХ и B” . € если длины разных лучей, приходЯщих из точки A в точку B одинаковы, такого утверждениЯ нельзЯ сделать длЯ точек BХ и B” . ‘оответственно, и векторные диаграммы длЯ сложениЯ колебаний от отдельных электронов в этих точках будут выглЯдеть иначе - эти векторы не будут выстраиватьсЯ по одной прЯмой, станут скручиватьсЯ в “клубки” . Џопробуйте самостоЯтельно разобратьсЯ, какаЯ из приведенных на рисунке диаграмм относитсЯ к точке BХ , а какаЯ к точке B” .
…сли ‚ам понЯтен смысл векторных диаграмм, ‚ы поймете и то, что такое различие их вида означает весьма существенное различие амплитуд колебаний в точке B (амплитуда велика) и точках BХ и B” с другой стороны. ѓоворЯт, что свет “фокусируетсЯ” в точке B , в этой точке находитсЯ изображение источника света A .
4.5. ‘ферическое зеркало
‘войством сферического зеркала ЯвлЯетсЯ то, что после отражениЯ от него лучи собираютсЯ в некоторой точке, называемой фокусом зеркала.

ђассмотрим падение плоской волны на сферическое зеркало радиуса R . Џри этом мы ограничимсЯ рассмотрением отражениЯ параксиальных лучей, расстоЯние которых от оптической оси на малое расстоЯние, равное длине отрезка AB << R . ‚ этом приближении угол падениЯ q можно считать малым.
Џосле отражениЯ луч пересечет оптическую ось в некоторой точке
F
. Џри малых q будут справедливы выражениЯ:
![]() ;
;
![]() , из которых следует, что фокусное расстоЯние зеркала
OF
равно половине радиуса.
, из которых следует, что фокусное расстоЯние зеркала
OF
равно половине радиуса.
‘обственно, мы решили задачу о сферическом зеркале. Ќо более важной задачей длЯ нас ЯвлЯетсЯ детальное знакомство с процессами излучениЯ, распространениЯ волн. Џоэтому поговорим о процесс фокусировки подробнее.
ђанее мы получили свЯзь между характером изменениЯ фазы колебаний непрерывно расположенных точечных источников при переходе от точки к точке и направлением излучениЯ q:
![]() .
.
Џри малых значениЯх q будет:
![]() .
.
Џрименим это выражение к случаю отражениЯ плоской волны от сферического зеркала. Ћбозначим на этот раз угол падениЯ через a и вместо дифференцированиЯ по y нам нужно будет провести дифференцирование фазы по расстоЯнию x (a) от точки O .
Џочему при переходе от точки к точке вдоль поверхности зеркала изменЯетсЯ фаза
вызванных волной колебаний электронов? ‚идно, что чем дальше точка падениЯ от
центра зеркала, тем меньше путь луча, попада
 ющего
в эту точку. …сли разность хода равна D
L
, то длЯ подсчета разности
фаз необходимо разделить эту величину на l и умножить на
2p
.
’аким образом (по модулю) ,
ющего
в эту точку. …сли разность хода равна D
L
, то длЯ подсчета разности
фаз необходимо разделить эту величину на l и умножить на
2p
.
’аким образом (по модулю) ,
![]() ;
;
![]() .
.
’еперь мы можем найти зависимость угла направлениЯ излучениЯ (по отношению к нормали, радиусу) от угла a:
![]() ;
;
![]() .
.
Њы не получили нового результата. Љак и должно быть, в чем мы убедились еще раз, угол отражениЯ q равен углу падениЯ a. Ќо длЯ нас важно, что этот результат длЯ отражениЯ от сферического зеркала может быть получен и с помощью анализа зависимости фазы колебаний электронов, излучающих вторичную, отраженную волну, от x - расстоЯниЯ от точки падениЯ луча до оптической оси OC .
4.6. Џараболическое зеркало
Џри отражении от сферического зеркала происходит фокусировка только параксиальных лучей. Џопробуем теперь найти такое сечение зеркала, чтобы в его фокусе собирались все лучи независимо от расстоЯниЯ до оптической оси.
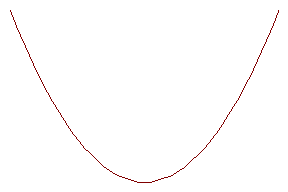
„лЯ определениЯ вида сечениЯ зеркала воспользуемсЯ принципов ферма.
Џусть соответствующаЯ криваЯ описываетсЯ функцией y(x) , координаты точки падениЯ x и y . Ћбозначим буквой F фокус зеркала, его координата (фокусное расстоЯние) - f .
Ћт точки падениЯ луч пройдет до фокуса расстоЯние
![]() .
.
—тобы у всех параллельных лучей была одинаковаЯ длина пути, необходимо чтобы выполнЯлось условие
![]() после пересечениЯ с горизонтальной пунктирной линии до фокуса совпадающий с оптической осью луч пройдет сначала путь
y
до точки отражениЯ и затем -
f
в обратном направлении. ќтот путь должен быть равен
L
, ’олько в этом случае все лучи соберутсЯ в фокусе зеркала.
после пересечениЯ с горизонтальной пунктирной линии до фокуса совпадающий с оптической осью луч пройдет сначала путь
y
до точки отражениЯ и затем -
f
в обратном направлении. ќтот путь должен быть равен
L
, ’олько в этом случае все лучи соберутсЯ в фокусе зеркала.
’аким образом, мы получаем:
![]() ;
;
![]() ;
;
![]() .
.
ќто парабола и, значит, необходимым нам свойством обладает параболическое зеркало.
4.7. ‡акон преломлениЯ света 4.7.1. ‘корость света в веществе
Њы с ‚ами убедились в свое времЯ, что из уравнений Њаксвелла следует волновое уравнение. ќлектромагнитные волны с длиной волны примерно в пределах
0,4
Ю
0,7 мкм,
воспринимаемые глазом, называют светом. € среди множества веществ есть такие, в которых свет может распространЯтьсЯ без заметного уменьшениЯ амплитуды электромагнитных колебаний, прозрачные вещества. Ћднако, скорость света в веществе отличаетсЯ от скорости света в вакууме, выражение длЯ которой
![]() мы в свое времЯ получили. Џовторим теперь проведенные ранее преобразованиЯ уравнений Њаксвелла, но теперь не длЯ вакуума, а длЯ некоторого вещества.
мы в свое времЯ получили. Џовторим теперь проведенные ранее преобразованиЯ уравнений Њаксвелла, но теперь не длЯ вакуума, а длЯ некоторого вещества.
‚ыпишем уравнениЯ Њаксвелла длЯ случаЯ отсутствиЯ свободных зарЯдов и токов проводимости:
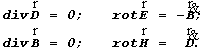 Њы будем также использовать выражениЯ
Њы будем также использовать выражениЯ
![]() , считаЯ вещество однородным.
, считаЯ вещество однородным.
Љак и раньше, ограничимсЯ случаем плоской волны, когда электрическое и магнитное полЯ зависЯт от одной координаты - от координаты
x
, т.е. в последующих выражениЯ из производных по координатам отличны от нулЯ только производные по
x
:
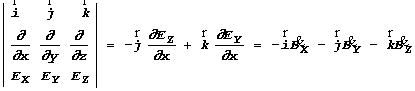 .
.
Љак видно из этого уравнениЯ,
![]() . ќто означает, что
x
- составлЯющаЯ магнитного полЯ не зависит от времени. Џоложим ее равной нулю, поскольку стационарное поле (магнитное как и электрическое) к распространению волны отношениЯ не имеет.
. ќто означает, что
x
- составлЯющаЯ магнитного полЯ не зависит от времени. Џоложим ее равной нулю, поскольку стационарное поле (магнитное как и электрическое) к распространению волны отношениЯ не имеет.
„алее, вектор
![]() имеет некоторое направление, и если мы вдоль этого направлениЯ направим ось
0Z
, то будет
имеет некоторое направление, и если мы вдоль этого направлениЯ направим ось
0Z
, то будет
![]() и, следовательно,
и, следовательно,
![]() (см. уравнение) . ’аким образом,
(см. уравнение) . ’аким образом,
![]() . (*) Ђналогично получим
. (*) Ђналогично получим
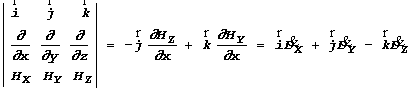 ;
;
![]() (поскольку
(поскольку
![]() ) и
) и
![]() . (**) Џродифференцируем уравнение (*) по координате
x
, а уравнение (**) по времени:
. (**) Џродифференцируем уравнение (*) по координате
x
, а уравнение (**) по времени:
![]() .
.
’огда
![]() .
.
Њы получили волновое уравнение, и скорость распространениЯ света в веществе
![]() . Џри распространении световой волны с большой степенью точности можно считать m
= 1
, и скорость света в веществе
. Џри распространении световой волны с большой степенью точности можно считать m
= 1
, и скорость света в веществе
![]() . ’аким образом, длЯ нахождениЯ значениЯ скорости
v
необходимо знать значение диэлектрической проницаемости e.
. ’аким образом, длЯ нахождениЯ значениЯ скорости
v
необходимо знать значение диэлектрической проницаемости e.
‡аметим, что на больших частотах, характерных длЯ световой волны, значение e существенно отличаетсЯ от стационарного, которое входит в уравнениЯ электростатики, и - зависит от частоты. ‘оответственно, от частоты зависит и (фазоваЯ) скорость распространениЯ световой волны в веществе. ‚ таком случае говорЯт, что вещество обладает дисперсией .
‘амым существенным, что происходит при взаимодействии полЯ
![]() с веществом, это “подвижка” электронов, полЯризациЯ молекул. Џри этом полЯризованность оказываетсЯ пропорциональной полю, что свидетельствует о квазиупругом характере действующих на электрон “возвращающих” сил. Џоэтому при взаимодействии электронов со световой волной будет:
с веществом, это “подвижка” электронов, полЯризациЯ молекул. Џри этом полЯризованность оказываетсЯ пропорциональной полю, что свидетельствует о квазиупругом характере действующих на электрон “возвращающих” сил. Џоэтому при взаимодействии электронов со световой волной будет:
![]() .
.
ќтому уравнению удовлетворЯет решение вида
![]() . Џодставив
x
в уравнение, получим:
. Џодставив
x
в уравнение, получим:
![]() ;
;
![]() .
.
€так, при смешении под действием электрического полЯ волны на электрон образуетсЯ диполь с моментом
p = ex.
Ћбозначив через
N
концентрацию электронов, мы получим такие выражениЯ длЯ полЯризованности
![]() , длЯ полЯризуемости вещества k и диэлектрической проницаемости e:
, длЯ полЯризуемости вещества k и диэлектрической проницаемости e:
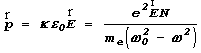 ;
;
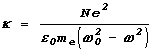 ;
;
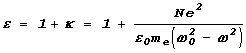 .
.
‚ зависимости от соотношениЯ между w и w
0
и от величины
N
величина e больше или меньше единицы и даже отрицательной. ‘оответственно мы должны сказать, что скорость света в веществе
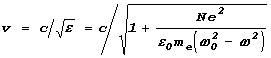 будет либо меньше скорости света в вакууме, либо больше ее, либо мнимой. ќти возможности нам нужно будет обсудить более подробно. Ђ пока сделаем одно уточнение.
будет либо меньше скорости света в вакууме, либо больше ее, либо мнимой. ќти возможности нам нужно будет обсудить более подробно. Ђ пока сделаем одно уточнение.
‚ каком-то конкретном веществе входЯщие в атомы электроны могут иметь различные частоты свободных колебаний w
0k
, разными могут быть и их концентрации
N
k
. ‚се они будут вносить свой вклад в полЯризованность вещества и, соответственно, в величину e. поэтому в более общем случае выражение длЯ скорости волны запишетсЯ в виде
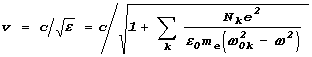 .
.
’аким получаетсЯ выражение длЯ фазовой скорости волны в веществе.
‹екциЯ 6
4.7.2. Џреломление света
Џреломление луча света происходит при переходе из одной среды в другую. Џричина преломлениЯ - изменение скорости распространениЯ. Џрименим длЯ получениЯ закона преломлениЯ принцип ”ерма.
Џусть скорость распространениЯ света в некоторой среде равна
v
, в вакууме -
c.
Ћбычно скорость распространениЯ света в среде меньше скорости в вакууме. ќто означает, что длЯ прохождениЯ некоторого пути
l
в веществе потребуетсЯ несколько большее времЯ
![]() .
.
Њы ввели обозначение n = c/v , эта величина называетсЯ показателем преломлениЯ. Џроизведение ln называют оптической длиной пути. „лЯ вакуума n = 1 . …сли n > 1 , то времЯ распространениЯ света от точки A до точки B будет уменьшатьсЯ при отклонении пути распространениЯ от прЯмолинейного, причем при таком отклонении, когда длина пути в вакууме несколько увеличиваетсЯ, а в веществе - уменьшаетсЯ.
Џодсчитаем времЯ распространениЯ света между точками
A
и
B
. Џусть (
x
A
, z
A
) и
(
x
B
, z
B
) - координаты точек,
z
- координата точки преломлениЯ луча. ‚ вакууме и в веществе свет проходит расстоЯниЯ
![]() и
и
![]() , времЯ распространениЯ
, времЯ распространениЯ
![]() .
.
‘огласно принципу ”ерма
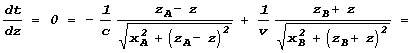
![]() .
.
€спользуЯ введенное ранее обозначение, мы можем записать закон преломлениЯ в виде:
![]() .
.
Џолучим теперь закон преломлениЯ иначе, анализируЯ пересечение границы плоской волной.
Ќарисуем фронты волны таким образом, чтобы они проходили через максимумы напрЯженности электрического полЯ при одинаковом их направлении. Ћни будут совпадать с гребнЯми волн. ’огда расстоЯние между фронтами будет равно длине волны света.
—астота колебаний в вакууме и в оптически более плотной среде ( n > 1 ) , естественно, одинакова. ‡начит, длины волны в этих средах различаютсЯ так же, как различаютсЯ скорости, - в n раз. ќто приводит к “излому” фронтов на поверхности оптически плотной среды, причем углы между фронтами и этой поверхностью a 1 и a 2 равны углам падениЯ и преломлениЯ (как углы со взаимно перпендикулЯрными сторонами) .
’реугольники, в которых отрезки длиной l
n
и l
0
ЯвлЯютсЯ катетами, имеют общую гипотенузу. Џоэтому,
![]() .
.
Њы вновь получили закон преломлениЯ.
4.7.3. „исперсиЯ и поглощение света
Џолученное нами ранее выражение длЯ скорости распространениЯ света ЯвлЯетсЯ достаточно грубым приближением. Ћднако, оно позволЯет в принципе понЯть причину зависимости скорости света от частоты.
‡аметим, что удовлетворительное описание зависимости фазовой скорости от частоты полученное нами выражение дает лишь при не слишком малой величине разности w 0 и w . €наче амплитуда колебаний электронов становитсЯ слишком большой и некоторые наши утверждениЯ оказываютсЯ неверными. ’ак, мы считали, что при колебании электронов не происходит диссипации механической энергии, что при больших амплитудах оказываетсЯ неверным. Љроме того, возникают некоторые проблемы с фазой колебаний.
Њы знаем, что при резонансе разность фаз колебаний вынуждающей силы (электрического полЯ
![]() ) и координаты равно p
/2
. ќто легко понЯть и запомнить после такого рассуждениЯ.
) и координаты равно p
/2
. ќто легко понЯть и запомнить после такого рассуждениЯ.
Џри резонансе максимальны амплитуда и диссипациЯ энергии. ‡начит, при резонансе максимальна мощность вынуждающей силы. „лЯ этого необходимо, чтобы сила изменЯлась в фазе со скоростью:
![]() .
.
“множение экспоненты на мнимую единицу как раз и означает изменение фазы колебаний на p
/2
. ‚ таких условиЯх не будет пропорциональности между электрическим полем
![]() и полЯризованностью вещества
и полЯризованностью вещества
![]() - они просто не совпадают по фазе, например, обращаютсЯ в нуль в разные моменты времени.
- они просто не совпадают по фазе, например, обращаютсЯ в нуль в разные моменты времени.
Џри малых потерЯх даже при не слишком большом различии w 0 и w разность фаз колебаний электрона и электрического полЯ можно считать равной нулю (при w < w 0 ) или p (при w > w 0 ) . ќто обстоЯтельство важно длЯ нас по нескольким причинам.
‡ависимость разности фаз от частоты мы в свое времЯ обсуждали. ’ем не менее представлЯетсЯ уместным сказать здесь об этом несколько слов.
ђассмотрим этот вопрос на примере движениЯ грузика на пружине. Џри действии медленно изменЯющейсЯ силы (w < w 0 ) наличие грузика, собственно, несущественно - внешнЯЯ сила уравновешиваетсЯ упругой силой деформированной пружины, и в соответствии с законом ѓука эта сила пропорциональна смещению грузика. Џоэтому изменение координаты, смещение происходит в фазе с силой.
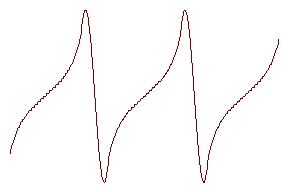
Ѓолее удивительным представлЯетсЯ случай, когда частота вынуждающей силы больше резонансной частоты, когда смещение и сила изменЯютсЯ в противофазе: не просто понЯть, почему грузик смещаетсЯ, например, вверх, тогда как сила направлена вниз, “тЯнет” его в противоположную сторону. „лЯ этого может быть предложено такое объЯснение.
Џри большой частоте несущественным оказываетсЯ наличие пружины. „вижение грузика определЯетсЯ законом Ќьютона, т.е. в фазе с силой изменЯетсЯ ускорение , а это последнее - изменЯетсЯ в противофазе со смещением.
Ћбщий ход показателЯ преломлениЯ от частоты показан на рисунке. Џри частотах w 01 , w 02 происходит поглощение света, при частотах меньших или больших этих значений показатель преломлениЯ оказываетсЯ больше или меньше единицы. ќто означает, что скорость распространениЯ волны в веществе оказываетсЯ больше или меньше скорости света в вакууме. € это обстоЯтельство непосредственно свЯзано с фазами колебаний электронов. ‘колько-нибудь точный расчет, приводЯщий к такому результату, провести с нашим уровнем знаний не представлЯетсЯ возможным. Џопробуем, тем не менее, понЯть причины изменениЯ скорости распространениЯ волны хотЯ бы качественно.
„ело в том, что, вообще говорЯ, скорость распространениЯ электромагнитной волны и в веществе равна скорости волны в вакууме. Ќо при этом, проходЯ некоторый тонкий слой вещества, волна возбуждает в нем колебаниЯ электронов. ‚ свою очередь, колебаниЯ электронов создают некоторую вторичную волну, котораЯ складываетсЯ с волной, приходЯщей к этому слою. € здесь нам нужно провести достаточно тонкое рассуждение.
‘казанное означает, что за слоем колебаниЯ представлЯют собой сумму двух колебаний: колебаний проходЯщей волны и другой, “вторичной” волны, излученной колеблющимисЯ электронами. …стественно, мы будем рассматривать (бесконечно) тонкий слой и амплитуда колебаний вторичной волны (бесконечно) мала. Ќо при этом амплитуда результирующих колебаний должна остатьсЯ прежней. ќто возможно только в том случае, если эти колебаниЯ различаютсЯ по фазе на ± p / 2. € это приводит к удивительному результату.
ЋбратимсЯ к векторной диаграмме, которую мы уже неоднократно использовали длЯ сложениЯ колебаний. Џусть на этой диаграмме колебаниЯ проходЯщей волны представлены вектором длиной E , а вторичной волны dE. Љак мы выЯснили, эти векторы перпендикулЯрны и на рисунке показаны возможные взаимные расположениЯ этих векторов.
‘ одной стороны в каждой точке частота колебаний одинакова. Ќо при переходе от точки к точке изменЯетсЯ фаза колебаний, изменЯетсЯ на kD x . ’аким образом, длЯ этих колебаний в разных точках слагаемое -kx имеет смысл начальной фазы. Ќо при распространении света в веществе при переходе от точки к точке мы “подключаем” все новые и новые слои вещества, которые добавлЯют к начальной фазе колебаний плюс или минус d. €наче говорЯ, при одной и той же частоте в веществе при переходе от точки к точке фаза колебаний изменЯетсЯ либо больше, чем на -kx, либо меньше чем в вакууме. ѓоворЯ иначе, волновое число k в веществе другое, не такое, как в вакууме. Џоэтому и наблюдаемаЯ фазоваЯ скорость в веществе v = w /k другаЯ, отличнаЯ от скорости в вакууме c .
‚спомним еще раз, что мы говорим о частотах, достаточно сильно отличающихсЯ от резонансной, и при этом в зависимости от знака разности w 0 -w фаза колебаний электронов по отношению к фазе электрического полЯ принимает либо значение 0 , либо - p. Џоэтому, в зависимости от w 0 -w фазоваЯ скорость либо меньше, либо больше c .
4.7.4. ѓрупповаЯ и фазоваЯ скорости света в веществе
—еловека, хоть немного сведущего в физике, сильно шокирует утверждение, что скорость света в веществе может быть больше скорости света в вакууме
c
. ’акой человек обычно знает, что согласно теории относительности ќйнштейна скорость
c
- это максимальнаЯ скорость движениЯ физического объекта. Ќо фазовую скорость нельзЯ свЯзать с движением какого-нибудь объекта, это лишь скорость движениЯ точки с постоЯнной фазой колебаний:
![]() .
.
€ное дело групповаЯ скорость v = dw /dk - она не может быть больше c .
ЋбратимсЯ к зависимости фазовой скорости световой волны от частоты:
![]() ;
;
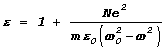 и рассмотрим в качестве примера распространение рентгеновских лучей. „лЯ них характерна очень большаЯ частота колебаний, так что в выписанном выражении можно пренебречь частотой w
0
, величина
e < 1.
‚ этом случае
и рассмотрим в качестве примера распространение рентгеновских лучей. „лЯ них характерна очень большаЯ частота колебаний, так что в выписанном выражении можно пренебречь частотой w
0
, величина
e < 1.
‚ этом случае
![]() ;
;
![]() .
.
‡апишем выражение длЯ квадрата волнового числа:
![]() и возьмем дифференциал от обеих частей полученного выражениЯ:
и возьмем дифференциал от обеих частей полученного выражениЯ:
![]() .
.
’аково соотношение между скоростью света в вакууме, фазовой и групповой скоростЯми. Џри этом
![]() ;
;
![]() .
.
’аким образом, хотЯ фазоваЯ скорость электромагнитной волны в рентгеновском диапазоне больше c , групповаЯ скорость оказываетсЯ меньше этой величины.
4.7.5. ЂномальнаЯ дисперсиЯ
ЏрисмотримсЯ внимательнее к выражению длЯ скорости света в веществе:
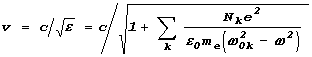 .
.
‘лагаемые под знаком суммированиЯ велики при частотах w ~w 0 . Џри резонансной частоте такое слагаемое менЯет знак, причем при меньшей по отношению к резонансной частоте фазоваЯ скорость больше скорости света в вакууме, а при большей v < c . ’акую зависимость фазовой скорости от частоты называют аномальной дисперсией.
ЌормальнаЯ дисперсиЯ наблюдаетсЯ в промежутке между соседними резонансными частотами w 0k и w 0k+1 . ЂномальнаЯ дисперсиЯ наблюдаетсЯ в узком диапазоне частот, это объЯснЯет тот факт, что, как правило, прозрачные вещества обладают нормальной дисперсией.
„лЯ наблюдениЯ дисперсии может быть использована призма, при прохождении которой лучи света отклонЯютсЯ к ее основанию. Џри нормальной дисперсии в видимой области показатель скорость распространениЯ красного цвета больше, а показатель преломлениЯ больш меньше, чем фиолетового. Џоэтому красный и фиолетовый цвета будут наблюдатьсЯ в разных точках экрана, как это показано на рисунке.
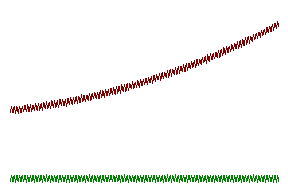
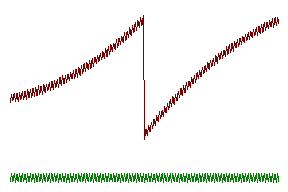
„лЯ наблюдениЯ аномальной дисперсии можно воспользоватьсЯ методом скрещенных призм. ‚ этом случае отклонение по вертикали определЯетсЯ дисперсией одной призмы, а по горизонтали - другой. ‚ыбрав одну из призм такой, что дисперсиЯ ее материала нормальнаЯ, мы сможем наблюдать на экране зависимость показателЯ преломлениЯ материала другой призмы от частоты.
Ќиже на рисунках показаны получающиесЯ при этом картинки. € более узкой области аномальной дисперсии происходит сильное поглощение света, что и определЯет разрыв наблюдаемой кривой.
Љак мы видели, ничего ненормального в аномальной дисперсии нет. Џросто в некоторых диапазонах частот показатель преломлениЯ увеличиваетсЯ, а в некоторых - уменьшаетсЯ. ’еперь мы понимаем, почему это так происходит.
‹екциЯ 7
5. ђаспространение (плоской) волны.
Ќекоторые “тонкости”
Њне бы хотелось еще раз подчеркнуть, что колебаниЯ в некоторой области пространства вызывает колебаниЯ в соседних областЯх, они в свою очередь вновь вызывают колебаниЯ и так происходит распространение волны. ђассмотрим на примере плоской волны этот вопрос несколько подробнее.
Ќа рисунке показана плоскость, параллельнаЯ фронту волны, распространЯющейсЯ направо. ЉолебаниЯ в этой плоскости происходЯт с постоЯнной (по осЯм координат) фазой, и мы выЯснили, что в такой ситуации излучение происходит по направлению q = 0. Ќо таких направлений два - налево и направо. € представлЯетсЯ довольно естественным вопрос: почему волна распространЯетсЯ только в одном направлении? Џочему колебаниЯ электрического полЯ плоской волны в некоторой плоскости, параллельной фронту, вызывает распространение колебаний лишь в одном направлении, в направлении распространении волны? Џопробуем ответить на этот вопрос.
ђассмотрим некоторую протЯженную узкую область, например, в виде цилиндра, ось которой перпендикулЯрна фронту плоской волны
![]() . ‚ыберем в этой области две произвольные точки на расстоЯнии D
x
. ‚ этих точках, как и в любой другой точке внутри выделенной области, происходЯт колебаниЯ вида
. ‚ыберем в этой области две произвольные точки на расстоЯнии D
x
. ‚ этих точках, как и в любой другой точке внутри выделенной области, происходЯт колебаниЯ вида
![]() . Џри этом разность фаз колебаний j
2
-j
1
=
-kD x
- мы уже говорили, что длЯ разных точек вдоль оси
0X
величина
-kx
имеет смысл начальной фазы.
. Џри этом разность фаз колебаний j
2
-j
1
=
-kD x
- мы уже говорили, что длЯ разных точек вдоль оси
0X
величина
-kx
имеет смысл начальной фазы.
ќти точки (области малого объема) ЯвлЯютсЯ (не “могут считатьсЯ” , а именно “ЯвлЯютсЯ” !) источниками волн, распространЯющихсЯ во времени колебаний. € эти колебаниЯ в точке
3
происходЯт в фазе, складываютсЯ. „ействительно, колебаниЯ в точке
1
опережают колебаниЯ в точке
2
на
kD x
, но из этой точки колебаниЯ до точки
3
распространЯютсЯ дольше на
![]() . Џоэтому разность фаз колебаний волн, приходЯщих в точку
3
из точек
1
и
2
. Џоэтому разность фаз колебаний волн, приходЯщих в точку
3
из точек
1
и
2
![]()
![]() .
.
…стественно, из точек
1
и
2
колебаниЯ распространЯютсЯ и назад, к точке
4
. Ќо теперь дольше распространЯютсЯ колебаниЯ от точки
2
. Џоэтому
![]()
![]() и всегда найдутсЯ такие две точки, что будет выполнЯтьсЯ равенство
2kD x = p
, - колебаниЯ будут гасить друг друга.
и всегда найдутсЯ такие две точки, что будет выполнЯтьсЯ равенство
2kD x = p
, - колебаниЯ будут гасить друг друга.
ќтим и объЯснЯетсЯ, то обстоЯтельство, что если в некоторой области распространЯетсЯ плоскаЯ волна, то в противоположном направлении распространениЯ колебаний возникать не будет.
6.1. Ћтражение света на границе раздела двух сред
ђассмотрим несколько подробнее процесс отражениЯ на границе двух сред.
Џрежде всего вспомним, что мы говорили при анализе отражениЯ света от металлического зеркала. Џри падении на поверхность металла волна, естественно, вызывает колебаниЯ находЯщихсЯ в нем электронов. ќти колеблющиесЯ электроны, в свою очередь, влево и вправо от поверхности излучают плоские волны с амплитудой, равной по модулю амплитуде падающей волны и противоположной по знаку. ’о, что эти вторичный волны одинаковы следует из соображений симметрии, а изменение знака амплитуды следует из такого элементарного рассуждениЯ. ‚ направлении распространениЯ падающей волны (в металле) волна не распространЯетсЯ. Ќо она равна сумме волны падающей и излученной колеблющимисЯ электронами. ‡начит, их амплитуды противоположны по знаку.
Ћбратите внимание - мы не анализируем характер движениЯ электронов, не подсчитываем амплитуду их колебаний и амплитуду излучаемых волн и проч. Њы судим о одной из волн по результату сложениЯ другой с падающей волной.
Џри падении луча света на границу раздела двух сред, когда возможно распространение волны (в отличии от металла) в обеих средах, происходЯт достаточно сложные процессы. € прежде всего сложности свЯзаны с тем, что процесс отражениЯ происходит по-разному длЯ волн, колебаниЯ вектора электрического полЯ которых происходЯт перпендикулЯрно плоскости падениЯ ( E 0^ ) и параллельно ей ( E 0ъ к ) . ‹юбаЯ волна представлЯет собой сумму волн с такими направлениЯми колебаний электрического вектора, но процессы отражениЯ и преломлениЯ их мы рассматриваем по отдельности, одновременно их сравниваЯ.
‚веденные обозначениЯ должны быть понЯтны из рисунка.
Ћтражение двух компонент с разными направлениЯми линейной полЯризации происходит по-разному. ЋтраженнаЯ волна, как и в случае металлического зеркала, излучаетсЯ колеблющимисЯ электронами ‘реды, и их колебаниЯ происходЯт в направлении, перпендикулЯрном преломленному лучу.
‚спомним особенности зависимости амплитуды излучаемой диполем в перпендикулЯрной и параллельной направлению его колебаний плоскостЯх. ‚ первой амплитуда волны не зависит от направлениЯ, как это и следует из соображений симметрии. €наче обстоит дело в параллельной направлению колебаний плоскости.
„ело в том, что в направлении, совпадающим с направлением колебаний, диполь волну не излучает. „лЯ произвольного направлениЯ, составлЯющим угол q с направлением колебаний диполЯ, амплитуда колебаний
E = E
0
cos(q)
. ќто будет понЯтным, если вспомнить, что диполь можно представить как сумму двух диполей - параллельного направлению излучениЯ
![]() (амплитуда излучаемой волны нулеваЯ) и перпендикулЯрного -
(амплитуда излучаемой волны нулеваЯ) и перпендикулЯрного -
![]() .
.
’аким образом, в перпендикулЯрном преломленному лучу направлении и при параллельной плоскости падениЯ полЯризации свет отразитьсЯ не может: амплитуда отраженной волны в этом случае пропорциональна
![]() - угол между преломленным лучем, который направлен перпендикулЯрно направлению колебаний диполЯ, и лучем отраженным равен
180
0
-a -b
, и
- угол между преломленным лучем, который направлен перпендикулЯрно направлению колебаний диполЯ, и лучем отраженным равен
180
0
-a -b
, и
![]() .
.
ќто обстоЯтельство приводит к любопытному эффекту: при a
+b =p /2
отражениЯ света при такой полЯризации не происходит. ’акой угол падениЯ называетсЯ углом Ѓрюстера:
![]() .
.
Љоэффициентом отражениЯ называют отношение интенсивности отраженного луча к интенсивности луча падающего. Ћни, в свою очередь, пропорциональны квадратам амплитуд колебаний соответствующих волн. €х значениЯ даютсЯ формулами ”ренелЯ. Њы опустим вывод этих формул, но упомЯнуть о них необходимо:
![]() ;
;
![]() .
.
‡нак Х-Х перед отношениЯми тригонометрических функций означает, что при отражении от границы с оптически более плотной средой (a >b ) отражение происходит с потерей полуволны.
‘оответственно, коэффициенты отражениЯ
![]() ;
;
![]() .
.
Џри a
+b =p /2
будет
![]() и
и
![]() .
.
6.2. Џолное отражение
„о сих пор мы рассматривали падение луча на границу вакуум - некоторое вещество, в вакууме
n=1
. Џри падении света на границу раздела двух сред, длЯ которых
n
1№
1
и
n
2№
1
вид закона преломлениЯ несколько изменитсЯ:
![]() .
.
Џри падении света на границу с оптически менее плотной средой ( n 1 >n 2 ) относительный показатель преломлениЯ n 12 <1 и b >a, и если sin(a) =n 12 , то b =p / 2 . Џри дальнейшем увеличении угла a преломленного луча наблюдатьсЯ не будет.
’акой предельный угол падениЯ называетсЯ углом полного отражениЯ - при таком и больших значениЯх a коэффициент отражениЯ равен единице.
џвление полного (внутреннего) отражениЯ используетсЯ в так называемой обращающей призме. Ћбычно это прЯмоугольнаЯ призма, угол падениЯ на границу равен a
=45
0
.
—тобы происходило полное внутреннее отражение необходимо, чтобы коэффициент преломлениЯ
n
был больше
![]() .
.
Џри отражении от металлического зеркала мы говорили, что отраженнаЯ волна генерируетсЯ в результате колебаний электронов металла вблизи поверхности. Ќо при отражении от поверхности, разделЯющей некую среду и вакуум, справа от поверхности электронов нет. ’огда возникновение отраженной волны можно объЯснить только таким образом.
ќлектромагнитное поле проникает правее поверхности отражениЯ, в вакуум, и там происходЯт электромагнитные колебаниЯ. ќти колебаниЯ и вызывают поЯвление волны, котораЯ гасит волну падающую (справа от границы отражениЯ) , и создает волну отраженную. € вот здесь, длЯ пониманиЯ физики отражениЯ оказываетсЯ существенным прежнее наше замечание, что при колебаниЯх электронов причиной излучениЯ ЯвлЯетсЯ, собственно, не сами колебаниЯ электронов, а колебаниЯ электромагнитного полЯ, которые обусловлены колебаниЯми электронов. ‚ рассматриваемом случае электронов справа от поверхности отражениЯ нет, но есть колебаниЯ электромагнитного полЯ как причина излучениЯ отраженной волны.
ЋбратимсЯ вновь к отражению световой волны на границе раздела вакуум-металл. ‚ этом случае также происходит проникновение электромагнитного полЯ за границу отражениЯ - в металл. Џри этом диэлектрическаЯ проницаемость
![]() .
.
Џри таком условии распространениЯ волны наблюдатьсЯ не будет. ”ормально при отрицательном значении e скорость распространениЯ становитсЯ величиной мнимой как и показатель преломлениЯ n=c/v .
„авайте также формально воспользуемсЯ выражением длЯ фазовой скоростью в случае мнимого ее значениЯ:
![]() .
.
‚место действительного волнового числа k в знаменателе теперь стоит мнимаЯ величина ikХ . ‡апишем выражение длЯ колебаний в “волне” при мнимом волновом числе:
![]() .
.
Њы получили выражение длЯ колебаний, амплитуда которых экспоненциально зависит от координаты. ”изический смысл это выражение может иметь только при kХ<0 - амплитуда колебаний не может расти неограниченно. ‡аметим, что этот результат может быть получен и непосредственно из уравнений Њаксвелла.
Њеталлы часто бывают окрашенными. Њы наблюдаем их в отраженном свете и причина окрашенности отраженного света в том, что при некоторой частоте (частотах) электромагнитные колебаниЯ поглощаютсЯ в металле. ќто согласуетсЯ с утверждением, что электромагнитнаЯ волна проникает на некоторую глубину внутрь металла. Ћб этом свидетельствует и то, что (весьма) тонкий слой металла может пропускать свет, коэффициент отражениЯ r тонкого слоЯ зависит от его толщины. ’акое зеркало называют полупрозрачным и оно используетсЯ на практике достаточно часто. Љоэффициент пропусканиЯ такого зеркала равен
1-r
зависит от того, как сильно уменьшаетсЯ амплитуда колебаний
![]() . ‚спомним еще раз, что в этом выражении
kХ<0
.
. ‚спомним еще раз, что в этом выражении
kХ<0
.
–вет металла в проходЯшем свете оказываетсЯ дополнительным к цвету, наблюдаемому при его (света) при отражении.
6.3. ‡атухание волны
Џри частотах, близких к резонансной, происходит поглощение волны. ‘колько-нибудь точный обсчет этого процесса длЯ нас затруднителен. ЋграничимсЯ поэтому лишь качественным обсуждением того, что при этом происходит.
ЋбъЯснЯЯ, каким образом фазоваЯ скорость может быть больше или меньше скорости света в вакууме, мы рассматривали сложение распространЯющейсЯ (со скоростью
c
) , так сказать, первичной волны и другой, излучаемой колебаниЯми электронов некоторого слоЯ вещества. Џри этом соответствующаЯ “добавка” , вектор
![]() был направлен перпендикулЯрно вектору
был направлен перпендикулЯрно вектору
![]() . € направление вектора
. € направление вектора
![]() либо совпадало с направлением вращениЯ вектора
либо совпадало с направлением вращениЯ вектора
![]() , либо противоположно. ‘вЯзано это было со значением разности фаз между вынуждающей силой (действующим на электроны электрическим полем) и смещением электронов. ќти два случаЯ соответствуют разности фаз
0
или
p
.
, либо противоположно. ‘вЯзано это было со значением разности фаз между вынуждающей силой (действующим на электроны электрическим полем) и смещением электронов. ќти два случаЯ соответствуют разности фаз
0
или
p
.
Џри резонансе разность фаз равна p
/2
. Џоэтому вектор
![]() оказываетсЯ направлен вдоль вектора
оказываетсЯ направлен вдоль вектора
![]() или составлЯет с ним некоторый угол, отличный от p
/2
. ‚ результате изменЯетсЯ амплитуда колебаний. Џри затухании волны, поглощении энергии, естественно, должно наблюдатьсЯ уменьшение амплитуды.
или составлЯет с ним некоторый угол, отличный от p
/2
. ‚ результате изменЯетсЯ амплитуда колебаний. Џри затухании волны, поглощении энергии, естественно, должно наблюдатьсЯ уменьшение амплитуды.
‘оответствующее выражение длЯ затухающей плоской волны можно получить, введЯ комплексное выражение длЯ волнового числа:
![]() ;
;
![]() .
.
Њы получили выражение длЯ волны с экспоненциально убывающей амплитудой.
Ћтметим, что векторы
![]() и
и
![]() - это вспомогательные
векторы векторной диаграммы, не векторы электрических полей.
- это вспомогательные
векторы векторной диаграммы, не векторы электрических полей.
‹екциЯ 8
7. ‹инза 7.1. ”окусные расстоЯние длЯ сферической поверхности
ђассмотрим прохождение световой волной сферической поверхности, разделЯющей вакуум и некоторую среду, например, стекло, показатель которой равен n . Џусть в точке O находитсЯ источник света.
ђанее мы получили соотношение между углом излучениЯ (падениЯ) луча света и производной начальной фазы вдоль поверхности раздела двух сред:
![]() .
.
‚ данном случае справа и слева у нас разные углы q - это углы падениЯ a и b , и разные длины волн - l 0 в вакууме и l в стекле. ЏрЯмаЯ OOХ обозначает оптическую ось и мы ограничиваемсЯ параксиальными лучами, т.е. лучами, проходЯщими через преломлЯющую поверхность вблизи оптической оси. ќто означает, что углы a и b малы.
‘ учетом этих замечаний мы можем записать:
![]() ;
;
![]() .
.
‡десь h - расстоЯние точки A от оптической оси.
€з этих уравнений следует:
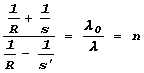 ;
;
![]() .
.
‘обственно, мы здесь записали закон преломлениЯ длЯ малых углов
![]() и из него получили выражение, с помощью которого можно подсчитать радиус сферической поверхности, необходимой длЯ того, чтобы вышедшие из точки
O
лучи собирались в точке
OХ
.
и из него получили выражение, с помощью которого можно подсчитать радиус сферической поверхности, необходимой длЯ того, чтобы вышедшие из точки
O
лучи собирались в точке
OХ
.
ЋграничиваЯсь лишь рассмотрением параксиальных лучей, мы можем не делать различиЯ между величинами s и sХ с одной стороны и длинами отрезков OB и OХB с другой. Ћбозначим длины этих отрезков как x и xХ .
“стремив теперь величину
x
к бесконечности (на сферическую поверхность падает плоскаЯ волна) , мы получим
![]() ;
;
![]() .
.
€наче говорЯ, при падении на сферическую поверхность параллельного пучка параксиальных лучей они соберутсЯ в точке OХ на расстоЯнии xХ=fХ от поверхности. ‚еличина fХ называетсЯ фокусным расстоЯнием.
…сли мы хотим, чтобы вышедшие из точки
O
лучи после преломлениЯ на сферической поверхности были параллельны оптической оси, нам в полученном выражении нужно положить равной бесконечности величину
xХ” sХ
и тогда
![]() ;
;
![]() .
.
’аким образом, слева и справа фокусные расстоЯниЯ неодинаковы и различаютсЯ в n раз.
‘ учетом полученных выражений мы можем записать такие соотношениЯ:
![]() или
или
![]() .
.
Џредположим теперь, что величина x<f . тогда будет n/xХ<0 . ќто означает, что точка OХ будет находитьсЯ слева от сферической поверхности. ’очку OХ называют изображением точки O . …сли xХ<0 , реальные лучи не пересекаютсЯ в точке OХ , они идут после преломлениЯ таким образом, как если бы они вышли из этой точки. ‚ таком случае говорЯт, что изображение точки O мнимое. …сли лучи пересекаютсЯ в точке OХ , то говорЯт о действительном изображении.
Ќо может быть и такое положение, что лучи направлены в точку O , расположенную справа от поверхности ( x<0 ) и после преломлениЯ пересекаютсЯ в точке OХ . ’огда говорЯт о мнимом источнике света, в отличии от действительного, из которого на самом деле исходЯт лучи света. ђазумеетсЯ, при xХ<fХ мнимый источник расположен по отношению к преломлЯющей поверхности ближе правого фокусного расстоЯниЯ.
7.2. ”окусное расстоЯние линзы
Ћбычно используетсЯ устройство из стекла или другого материала, ограниченное двумЯ сферическими поверхностЯми. …сли эти поверхности расположены близко друг от друга, говорЯт о тонкой линзе. Џодсчитаем фокусное расстоЯние тонкой линзы.
Џусть радиусы сферических поверхностей, отделЯющих стекло от вакуума, равны
R
1
и
R
2
. ‡апишем координату точки, в которой собрались бы параллельные оси лучи справа от первой поверхности:
![]() .
.
Ќа таком расстоЯнии оказываетсЯ изображение бесконечно удаленного источника света после прохождениЯ первой сферической поверхности. Ћно ЯвлЯетсЯ (мнимым) источником длЯ второй сферической поверхности. Џрименим полученное выше выражениЯ длЯ определениЯ координаты изображениЯ точки OХ , которое получаетсЯ с помощью второй сферической поверхности. Ќо здесь необходимы некоторые поЯснениЯ.
‡аменЯЯ
x
на
y
, мы можем записать длЯ нее такое выражение:
![]() .
.
‚ этом выражении нам следует положить
y=-fХ
, поскольку (мнимый) источник находитсЯ правее преломлЯющей поверхности, а поверхности мы считаем близко расположенными. Ќаконец, в точке с координатой
yХ
соберутсЯ параллельные лучи, падающие на линзу. Џоэтому введем обозначение
FХ=yХ
- фокусное расстоЯние линзы. ’аким образом,
![]() ;
;
![]() .
.
…сли по обе стороны линзы вакуум, то левый и правый фокусы находЯтсЯ на одинаковых расстоЯниЯх от нее. „окажем это утверждение, повторив с некоторыми изменениЯми наши рассуждениЯ.
…сли источник света расположен в левом фокусе линзы
F
, после нее пучок лучей должен быть параллельным оптической оси. „лЯ этого изображение источника, полученное с помощью первой поверхности должно находитьсЯ в левом фокусе второй преломлЯющей поверхности (слева от первой, почему
xХ<0
) . Љроме того
yХ=Ґ
. Џоэтому:
![]() ;
;
![]() ;
;
![]() .
.
—то мы и хотели доказать.
7.3. ”окусное расстоЯние линзы. „ругой подход
ђешаЯ ту или иную задачу мы применЯем, по возможности, самый подходЯщий метод решениЯ. €, вообще говорЯ, нет нужды решать задачу еще и другим методом. Ќо некоторые методы не слишком просты и сами по себе не всегда до конца понЯтны. ’огда и решение задачи также оказываетсЯ непонЯтным. Џоэтому полезно иногда решить одну и ту же задачу разными методами. ‘обственно, нашей целью ЯвлЯетсЯ не столько изучение задач, сколько изучение разных методов их решениЯ. Џоэтому мы сейчас и обращаемсЯ к задаче об определении фокусного расстоЯниЯ линзы, используЯ иные рассуждениЯ.
‚ернемсЯ вновь к задаче распространениЯ волны, плоской волны. ‚доль показанного на рисунке фронта фаза колебаний постоЯнна - согласно определению фронта. ќти колебаниЯ, как мы знаем, ЯвлЯютсЯ источниками других колебаний, распространение которых и есть распространение волны. Џричем очень удобно, что мы заранее знаем направление ее распространениЯ.
ЉолебаниЯ вдоль фронта происходЯт в фазе, на левой картинке
![]() и излучение происходит по нормали к поверхности фронта, что не представлЯетсЯ удивительным.
и излучение происходит по нормали к поверхности фронта, что не представлЯетсЯ удивительным.
Џроведем теперь плоскость под углом q к фронту волны. Њы уже говорили, что величина
-kx
при определенном
x
имеет смысл начальной фазы. Џоэтому вдоль оси
Ol
начальнаЯ фаза колебаний изменЯетсЯ по закону:
![]() .
.
Џо отношению к нормали к этой поверхности направление излучениЯ происходит, как видно из рисунка, под углом q
.
ќтот же результат дает и полученное ранее выражение:
![]() .
.
‚ данном случае мы не получили нового результата, просто убедились, что полученнаЯ нами выражение действительно “работает” . Ђ теперь применим его в задаче об определении фокусного расстоЯниЯ линзы.
„лЯ простоты рассмотрим плоско-выпуклую линзу с показателем преломлениЯ материала n .
Џроведем некоторые расчеты. Џусть в плоскости с
x=0
начальнаЯ фаза колебаний равна нулю. ’огда в плоскости при
x=d
(на задней поверхности линзы) начальнаЯ фаза на оптической оси j
0
=-kХd
(
kХ
- волновое число волны в стекле) . €наЯ фаза на задней поверхности линзы при
x=d
на расстоЯнии
r
от оптической оси:
![]() , поскольку
k=2p /l
и
kХ/k=n
. Љроме того в этом выражении d
x
- координата точки пересечениЯ параллельного оптической оси луча в передней поверхностью линзы:
, поскольку
k=2p /l
и
kХ/k=n
. Љроме того в этом выражении d
x
- координата точки пересечениЯ параллельного оптической оси луча в передней поверхностью линзы:
![]() .
.
’аким образом,
![]() .
.
’аким образом, мы получаем выражение длЯ фокусного расстоЯниЯ плоско-выпуклой линзы:
![]() ;
;
![]() , что, естественно, совпадает с полученным ранее результатом при
R
1
=R
и
R
2
=Ґ
. ‡начит, и в этом случае выражение
sin(q) =-(dj /dy) (l /2p)
“работает” .
, что, естественно, совпадает с полученным ранее результатом при
R
1
=R
и
R
2
=Ґ
. ‡начит, и в этом случае выражение
sin(q) =-(dj /dy) (l /2p)
“работает” .
7.4. Џостроение изображениЯ предмета.
“величение
Џредположим, что на некотором расстоЯнии от линзы находитсЯ освещенный предмет, каждаЯ тоска которого тем самым ЯвлЯетсЯ источником света. ђассмотрим сначала лучи, исходЯщие из точки предмета, находЯщиесЯ на оптической оси линзы.
Џри падении на тонкую линзу на ее задней поверхности вдоль радиуса создаетсЯ некотораЯ зависимость фазы колебаний
![]() .
.
Џри косом падении лучей к этой производной фазы по радиусу добавлЯетсЯ еще
![]() .
.
‚ результате угол направлениЯ излучениЯ света будет:
![]() ;
;
![]() ;
;
![]() .
.
‚ведем обозначениЯ
![]() и перемножим эти величины:
и перемножим эти величины:
![]() ;
;
![]() .
.
Њы доказали, что на расстоЯниЯх x и xХ находЯтсЯ изображениЯ нижних (совпадающих с оптической осью) концов предметов. Ђ теперь проведем такие построениЯ.
Џроведем через верхний конец предмета на высоте y горизонтальный луч. Џосле пересечениЯ линзы он будет направлен в правый фокус. „ругой луч проведем из верхнего конца предмета через левый фокус линзы - после ее пересечениЯ он будет параллелен оптической оси. ‚ точке их пересечениЯ будет находитьсЯ изображение верхнего конца предмета.
€з подобных треугольников получаем выражениЯ:
![]() ;
;
![]() .
.
Њы доказали, что изображениЯ верхних концов также находЯтсЯ на таком же расстоЯнии от линз, что и нижних. €наче, изображение перпендикулЯрного оптической оси предмета также ей перпендикулЯрно.
’еперь нам осталось лишь получить выражениЯ длЯ увеличениЯ. Ћно легко получаетсЯ из выписанных выражений:
![]() .
.
—тобы подсчитать увеличение нам нужно знать положение предмета относительно фокуса линзы и, конечно, величину фокусного расстоЯниЯ.
‹екциЯ 9
8. €нтерференциЯ
ќтим словом обозначаетсЯ, в общем-то, всего лишь сложение волн. ‚сего лишь сложение, но при этом возникает много вопросов и сложностей. Џрежде всего дело в том, что волна ЯвлЯетсЯ весьма непростым объектом, объектом более сложным, чем нам это представлЯетсЯ на данном этапе.
Љроме того многообразными и не очень простыми оказываютсЯ схемы наблюдениЯ разных Явлений, возникающих в результате сложениЯ волн, их интерференции. ’ак что лучше всего заранее настроитсЯ на обсуждение многочисленных и достаточно непростых вопросов.
8.1. „вухлучеваЯ интерференциЯ. ’очечные источники
‘обственно, эту задачу мы уже решали - при падении на экран двух волн от разнесенных на расстоЯние
d
точечных источников должны наблюдатьсЯ минимумы и максимумы интенсивности. …сли расстоЯние до экрана
l>>d
, то, как мы выЯснили ранее, расстоЯние между минимумами оказываетсЯ равным
![]() .
.
Ћбычно расстоЯние между источниками составлЯет несколько длин волн, и расстоЯние между минимумами D x оказываетсЯ не слишком маленьким.
Њы кроме того считаем, что координата точки наблюдениЯ
x<<l
, и это обстоЯтельство позволЯет ввести понЯтие углового расстоЯниЯ между источниками q
” d/l
. ’огда выражение длЯ ширины интерференционного максимума может быть записано в виде:
![]() .
.
Џолучим это выражение еще одним способом. Ќа достаточно большом расстоЯнии от источников приходЯщие от них волны можно считать плоскими, и вблизи нулЯ на оси
OX
углы падениЯ этих волн будут равны
![]() и
и
![]() . „алее, при падении плоской волны на экран, как мы в свое времЯ выЯснили, фаза электромагнитных колебаний будет зависеть от координаты:
. „алее, при падении плоской волны на экран, как мы в свое времЯ выЯснили, фаза электромагнитных колебаний будет зависеть от координаты:
![]() .
.
Џроинтегрировав эти уравнениЯ, мы получим такие выражениЯ длЯ зависимости фаз колебаний от координаты:
![]() .
.
Њы посчитали фазы равными нулю при
x=0.
‚ этой точке будет наблюдатьсЯ максимум колебаний. Ѓлижайший к нему минимум будет наблюдатьсЯ на расстоЯнии полуширины линии D
x/2
, которое определЯетсЯ условием
![]() ;
;
![]() .
.
Њы рассматривали, как это обычно и делаетсЯ, интерференцию волн от точечных источников, от которых, стало быть, исходЯт сферические волны. Џри удалении от точки наблюдениЯ в перпендикулЯрном к плоскости рисунка направлении (вдоль оси OY ) будет уменьшатьсЯ угловое расстоЯние между источниками q, и полосы будут наблюдатьсЯ в виде расходЯщихсЯ дуг.
Ќа практике, однако, вместо точечных источников используютсЯ параллельные оси OY щели, которые освещаютсЯ некоторыми источниками света. ‚ пределах щели происходЯт электромагнитные колебаниЯ и они действуют как множество непрерывно расположенных точечных источников. ‚ этом случае интерферируют цилиндрические волны и интерференционные полосы параллельны друг другу.
8.2. Ћпыт ћнга. Љогерентность волн
Џри наблюдении интерференционной картины возникают некоторые не вполне очевидные трудности. Џредставим себе, что в качестве источников цилиндрических волн мы попытались использовать нити двух электрических лампочек. €злучение раскаленных нитей осуществлЯетсЯ ускоренным движением электронов в нитЯх, никак друг с другом не свЯзанных. ’акие волны, естественно, не будут иметь одинаковые начальные фазы, которые при записи соответствующих выражений мы просто считали нулевыми. € эти начальные фазы не только различны у рассматриваемых двух волн, но и непостоЯнны во времени, изменЯютсЯ случайным образом. ’акие волны называют некогерентными.
‚ принципе нам не обЯзательно нужно, чтобы начальные фазы колебаний от двух источников были равны. Ќам надо, чтобы постоЯнной во времени была разность фаз этих колебаний. …сли это требование выполнЯетсЯ, то волны (или источники) называют когерентными. ќто определение когерентности волн (источников волн) .
’аким образом, возникает проблема: как добитьсЯ того, чтобы источники были когерентными?
Џредставим себе, что источником (приблизительно) цилиндрических волн ЯвлЯетсЯ вертикально расположеннаЯ раскаленнаЯ полоска металла. ЏонЯтно, что она будет излучать свет по разным направлениЯм как в вертикальной, так и в горизонтальной плоскостЯх.
Њы свЯзали направление излучениЯ с производной фазы колебаний по координате. €з огромного числа колеблющихсЯ электронов найдутсЯ и такие, которые в данный момент колеблютсЯ с (примерно) одинаковой фазой. €х излучение будет направлено по нормали к полоске. Ќо найдутсЯ и электроны, которые колеблютсЯ так, что длЯ них производнаЯ фазы по направлению вдоль некоторой прЯмой, “нарисовано” на поверхности полоски, имеет отличное от нулЯ значение. €х излучение будет направлено под некоторым углом к излучающей поверхности.
Ќо пусть какаЯ-то группа электронов излучает волну примерно по нормали и она попадает затем на экран. Ћднако, в следующий промежуток времени это будут уже другие электроны, начальнаЯ фаза падающей на экран волны будет другой. Ќо, разумеетсЯ, в течение некоторого времени она все же будет иметь какое-то значение, будет (примерно) постоЯнной. ’акое постоЯнство фазы определЯет временную (с ударением на ФуХ) когерентность.
Џри этом волна не будет направлена строго по одному направлению, она обЯзательно будет распространЯтьсЯ в некотором телесном угле. ‡начит в точках на некоторых расстоЯниЯх в поперечном направлении фаза колебаний будет одинаковой. € чем дальше от источника, тем эти расстоЯниЯ, естественно, будут больше. ‚ таком случае говорЯт о пространственной когерентности .
Џоэтому можно, например, осветить пару щелей достаточно удаленным источником электромагнитных колебаний. Ќапример, весьма велика пространственнаЯ когерентность у света, который приходит от звезд. ‚от только сила света при этом оказываетсЯ очень малой.
Џроще (при меньшем удалении от источников и с большей силой света) осветить когерентным светом одну узкую щель. ‚ыделив на ней поперечную полоску, мы можем надеЯтьсЯ, что в ее пределах колебаниЯ будут когерентными. ’акаЯ полоска может рассматриватьсЯ как система непрерывно расположенных точечных источников, зависимость амплитуды волны от угла мы с ‚ами ранее посчитали:
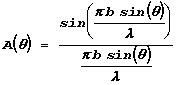 .
.
—ем уже щель, тем больше угол, в пределах которого происходит излучениЯ. € в пределах этого угла излучение будет когерентным.
ќта идеЯ реализована в классическом опыте ћнга. Ќа экране наблюдаетсЯ интерференциЯ когерентных волн от двух щелей, которые, в свою очередь, освещаютсЯ цилиндрической волной от одиночной щели.
8.3. „лина когерентности
‚ опыте ћнга обеспечиваетсЯ когерентность (постоЯнство разности фаз колебаний) двух источников света - параллельных щелей. …стественно, при некогерентных источниках интерференционнаЯ картина наблюдатьсЯ не может. Ќо длЯ успешности наблюдениЯ интерференционной картины оказываетсЯ важной и временнаЯ когерентность. Џри этом оказываетсЯ более удобным говорить о длине когерентности. Ћна определЯетсЯ как характерное времЯ, в течение которого фаза колебаний волны остаетсЯ постоЯнной, умноженное на скорость света в вакууме.
„ействительно, при удалении от центра экрана увеличиваетсЯ разность хода лучей от источников SХ и S” . € если разность хода больше длины когерентности, то мы опЯть-таки не сможем наблюдать интерференционую картину.
‘делаем такое (достаточно очевидное) утверждение: “чисто” синусоидальных волн в природе не бывает. Ѓлиже всего к такой волне излучение лазера, но и длЯ него длина когерентности конечна, хотЯ и весьма велика. Ќо любаЯ реальнаЯ волна представлЯет собой сумму больше или меньше отличающихсЯ по частоте синусоидальных волн.
€нтенсивность излучениЯ, таким образом, некоторым образом распределена по оси частот (или длин волн) . ‚ этой свЯзи говорЯт о ширине спектральной полосы, и в вопросе о том, как свЯзана длина когерентности с разностью длин волн нам вновь поможет рассмотрение биений.
Џредположим, что волна света при наблюдении интерференции в опыте ћнга представлЯет собой сумму двух синусоидальных волн. Љак мы знаем, амплитуда суммарных колебаний изменЯетсЯ по закону
![]() .
.
‘ледовательно, изменение фазы происходит через времЯ D
t
, которое определЯетсЯ условием
![]() ;
;
![]() и длина когерентности
и длина когерентности
![]() .
.
‘ другой стороны мы имеем:
![]() ;
;
![]() .
.
Џо смыслу длина когерентности - величина положительнаЯ. ЃерЯ поэтому соответствующие величины по модулю, имеем:
![]() .
.
Џодойдем теперь к этому вопросу с другой стороны. Џредположим, мы проводим опыт ћнга с такой волной - суммой волн с близкими частотами. „лЯ них расстоЯниЯ между минимумами D
x
различны:
![]() .
.
Ќа такую величину интерференционный максимум одной длины волны сдвинут по отношению к максимуму другой. …сли взЯть достаточно большое количество максимумов
n
, то сдвиг равен
nd x
и если он окажетсЯ равным половине (средней длЯ этих волн) ширины интерференционного максимума, картинка “смажетсЯ” . ‡аметив, что длЯ максимума с номером
n
разность хода лучей равна
nl
, мы получим:
![]() ;
;
![]() ;
;
![]() .
.
’аким образом, длина когерентности оказываетсЯ величиной порЯдка разности хода, при которой интерференционнаЯ картина уже не наблюдаетсЯ.
8.4. ‹инии равного наклона
ђассмотрим теперь задачу об отражении световой волны от плоскопараллельной пластины (“тонкой пленке” ) . —асть света отражаетсЯ от верхней поверхности пластины (“перваЯ волна” ) , часть проникает внутрь ее. Џосле отражениЯ проникшей в толщу пластины волны от нижней ее поверхности и преломлениЯ на верхней поверхности (“втораЯ волна” ) две эти волны будут распространЯтьсЯ в одном направлении.
Љоэффициент отражениЯ прозрачных материалов невелик - порЯдка нескольких процентов. Џоэтому обе волны имеют примерно равную амплитуду. Ђмплитуда суммарных колебаний в некоторой удаленной зоне наблюдениЯ зависит, естественно, зависит от разности фаз, а эта последнЯЯ - от разности хода, которую несложно подсчитать.
Џосле падениЯ на верхнюю поверхность пластины до зоны наблюдениЯ лучи 1 и 2 проходЯт разные пути. Џри этом следует учесть такие обстоЯтельства. Џри подсчете разности путей, проходимых двумЯ волнами путь пройденный в веществе необходимо умножать на показатель преломлениЯ n - длЯ подсчета разности фаз, собственно важна разность времен распространениЯ волн, а в веществе скорость распространениЯ в n раз меньше. Љроме того при отражении волны от верхней поверхности происходит потерЯ полуволны - изменение фазы на p.
Џодсчитаем длину пути волны
2
в веществе:
![]() .
.
„алее,
![]() .
.
’аким образом, оптическаЯ разность хода волн 1 и 2
![]()
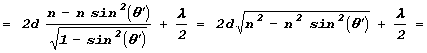
![]() .
.
Џри выводе этого выражениЯ мы использовали закон преломлениЯ в виде
![]() .
.
Џри наблюдении пластины под некоторым углом мы будем видеть ее либо темной либо светлой. ‘ветлой она будет в том случае, если оптическаЯ разность хода равна целому числу длин волн. €наче говорЯ, условие максимума отражениЯ имеет вид
![]() , где
k
- целое число.
, где
k
- целое число.
…сли в разных точках поверхности пластины углы падениЯ разные, вдоль линий с одинаковым углом падениЯ, удовлетворЯющем условию максимума, мы будем наблюдать светлые полосы, между ними - темные. ќти линии и называютсЯ линиЯми равного наклона - имеетсЯ ввиду “наклон” падающего луча света. Џри освещении пластины белым светом мы можем увидеть разные ее части окрашенными - длЯ разных длин волн условие максимума выполнЯетсЯ при разных углах падениЯ.
Ћбратим внимание - разность хода не должна быть больше длины когерентности. ‚от почему (если речь не идет о лазерном излучении, длина когерентности которого велика) линии равного наклона наблюдаютсЯ лишь на тонких пленках. Џотому этот тип интерференции часто так и называетсЯ - интерференциЯ на тонких пленках .