

1. Áýòà-ôóíêöèè 6
Бэта – функции определяются интегралом Эйлера первого рода:
сходятся при
![]() .Полагая
.Полагая
![]() =1 – t получим:
=1 – t получим:
![]() = -
= -
![]() =
=
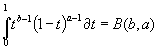
т.e. аргумент
![]() и
и
![]() входят в
входят в
![]() симетрично. Принимая во внимание тождество
симетрично. Принимая во внимание тождество
![]()
по формуле интегрирования почестям имеем
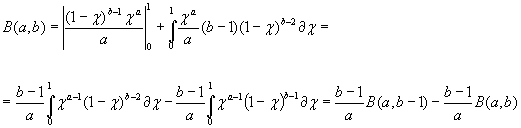
Откуда
7
При целом b = n последовательно применяя(1.2)
Получим
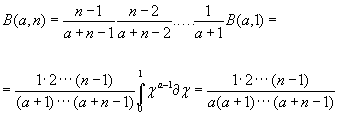 (1.3)
(1.3)
при целых
![]() = m,
= m,
![]() = n,имеем
= n,имеем
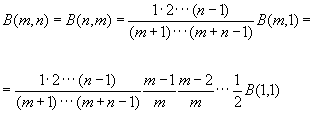
но B(1,1) = 1,следовательно:
![]()
![]()
![]()
Положим в (1.1)
![]() .Так как график функции
.Так как график функции
![]() симметрична относительно прямой
симметрична относительно прямой
![]() ,то
,то
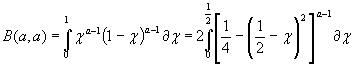
8
и в результате подстановки
![]() ,получаем
,получаем
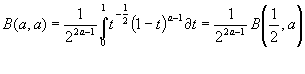
полагая в(1.1)
![]() ,откуда
,откуда
![]() ,получим
,получим
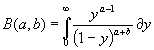 (1.4)
(1.4)
разделяя интеграл на два в пределах от 0 до 1 и от 1 до
![]() и применение ко второму интегралу подстановки
и применение ко второму интегралу подстановки
![]() ,получим
,получим
![]() =
=
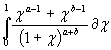
2. Ãàììà-ôóíêöèÿ 9
Гамма функцию определяет интеграл Эйлера второго рода
G (a) =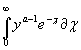
сходящийся при
![]() 0.Положим
0.Положим
![]() =ty,t > 0 ,имеем
=ty,t > 0 ,имеем
G
(a) =
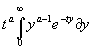
и после замены
![]() , через
, через
![]() и t через 1+t ,получим
и t через 1+t ,получим
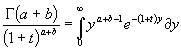
Умножая это равенство и интегрируя по t и пределах от 0 до
![]() , имеем:
, имеем:
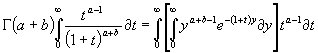
или на основании (1.4) и после изменения в правой части порядка интегрирования ,получаем:
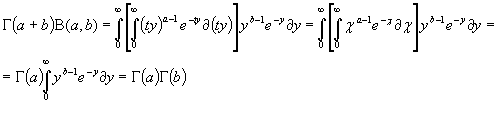
10
откуда
![]() (2.2)
(2.2)
заменяя в (2,1)
![]() ,на
,на
![]() и интегрируем по частям
и интегрируем по частям
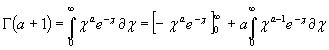
получаем рекурентною формулу
![]()
так как
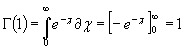
но при целом
![]() имеем
имеем
![]() (2.4)
(2.4)
то есть при целых значениях аргумента гамма-функция превращается в факториал.Порядок которого на единицу меньше взятого значения аргумента.При n=1 в (2.4) имеем
![]()
3. Производная гамма функции 11
Интеграл
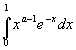
![]()
сходится при каждом
![]() ,поскольку
,поскольку
![]() ,и интеграл
,и интеграл
![]()
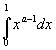 при
при
![]() сходится.
сходится.
В области
![]() , где
, где
![]() - произвольное положительное число, этот интеграл сходится равномерно, так как
- произвольное положительное число, этот интеграл сходится равномерно, так как
![]() и можна применить признак Веерштраса. Сходящимся при всех значениях
и можна применить признак Веерштраса. Сходящимся при всех значениях
![]() является и весь интеграл
является и весь интеграл
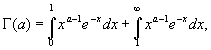 так как и второе слогаемое правой части является интегралом, заведомо сходящимся при любом
так как и второе слогаемое правой части является интегралом, заведомо сходящимся при любом
![]() .Легко видеть что интеграл сходится по
.Легко видеть что интеграл сходится по
![]() в любой области
в любой области
![]() где
где
![]() произвольно.Действительно для всех указаных значений
произвольно.Действительно для всех указаных значений
![]() и для всех
и для всех
![]()
![]() ,и так как
,и так как
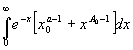 сходится, то выполнены условия признака Веерштрасса. Таким образом , в области
сходится, то выполнены условия признака Веерштрасса. Таким образом , в области
![]() интеграл
интеграл
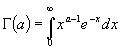 cходится равномерно.
cходится равномерно.
![]()
Отсюда вытекает непрерывность гамма функции при
![]() .Докажем дифференцируемость этой функции при
.Докажем дифференцируемость этой функции при
![]() .Заметим что функция
.Заметим что функция
![]() непрерывна при
непрерывна при
![]() и
и
![]() , и покажем ,что интеграл :
, и покажем ,что интеграл :
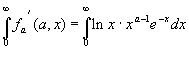
сходится равномерно на каждом сегменте
![]() ,
,
![]() . Выберем число
. Выберем число
![]() так , чтобы
так , чтобы
![]() ; тогда
; тогда
![]() при
при
![]() .Поэтому существует число
.Поэтому существует число
![]() такое , что
такое , что
![]() и
и
![]() на
на
![]() .Но тогда на
.Но тогда на
![]() справедливо неравенство
справедливо неравенство
![]()
и так как интеграл
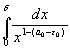 сходится, то интеграл
сходится, то интеграл
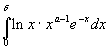 сходится равномерно относительно
сходится равномерно относительно
![]() на
на
![]() . Аналогично для
. Аналогично для
![]() существует такое число
существует такое число
![]() , что для всех
, что для всех
![]() выполняется неравенство
выполняется неравенство
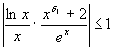 . При таких
. При таких
![]() и всех
и всех
![]() получим
получим
![]() , откуда в силу признака сравнения следует , что интеграл
, откуда в силу признака сравнения следует , что интеграл
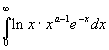 сходится равномерно относительно
сходится равномерно относительно
![]() на
на
![]() . Наконец , интеграл
. Наконец , интеграл
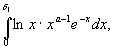
в котором подынтегральная функция непрерывна в области
![]() , очевидно, сходится равномерно относительно
, очевидно, сходится равномерно относительно
![]() на
на
![]() . Таким образом , на
. Таким образом , на
![]() интеграл
интеграл
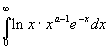
сходится равномерно , а, следовательно , гаммма функция бесконечно дифференцируема при любом
![]() и справедливо равенство
и справедливо равенство
![]()
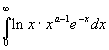 .
.
Относительно интеграла
![]() можна повторить теже рассуждения и заключить, что
можна повторить теже рассуждения и заключить, что
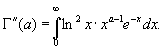
По индукции доказывается , что Г-функция бесконечно дифференцируема при
![]() и для ее я
и для ее я
![]() -ой производной справедливо равенство
-ой производной справедливо равенство
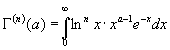
Изучим теперь поведение
![]() - функции и построим єскиз ее графика .
- функции и построим єскиз ее графика .
Из выражения для второй производной
![]() -функции видно, что
-функции видно, что
![]() для всех
для всех
![]() . Следовательно,
. Следовательно,
![]() возрастает. Поскольку
возрастает. Поскольку
![]() , то по теореме Роля на сегменте [1,2]производная
, то по теореме Роля на сегменте [1,2]производная
![]() при
при
![]() и
и
![]() при
при
![]() , т. е. Монотонно убывает на
, т. е. Монотонно убывает на
![]() и монотонно возрастает на
и монотонно возрастает на
![]() . Далее , поскольку
. Далее , поскольку
![]() , то
, то
![]() при
при
![]() . При
. При
![]() из формулы
из формулы
![]() следует , что
следует , что
![]() при
при
![]() .
.
14
Равенство
![]() , справедливое при
, справедливое при
![]() , можно использовать при распространении
, можно использовать при распространении
![]() - функции на отрицательное значение
- функции на отрицательное значение
![]() .
.
Положим для
![]() , что
, что
![]() . Правая часть этого равенства определена для
. Правая часть этого равенства определена для
![]() из
(-1,0)
. Получаем, что так продолженная функция
из
(-1,0)
. Получаем, что так продолженная функция
![]() принимает на (-1,0) отрицательные значения и при
принимает на (-1,0) отрицательные значения и при
![]() , а также при
, а также при
![]() функция
функция
![]() .
.
Определив таким образом
![]() на
на
![]() , мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением
, мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением
![]() окажется функция, принимающая положительные значения и такая, что
окажется функция, принимающая положительные значения и такая, что
![]()
![]()
![]() при
при
![]() и
и
![]() . Продолжая этот процесс, определим функцию
. Продолжая этот процесс, определим функцию
![]() , имеющею разрывы в целочисленных точках
, имеющею разрывы в целочисленных точках
![]() (см. рис.1)
(см. рис.1)
Отметим еще раз, что интеграл
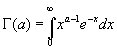
определяет Г-функцию только при положительных значениях
![]() , продолжение на отрицательные значения
, продолжение на отрицательные значения
![]() осуществлено нами формально с помощью формулы приведения
осуществлено нами формально с помощью формулы приведения
![]()
![]() .
.
15
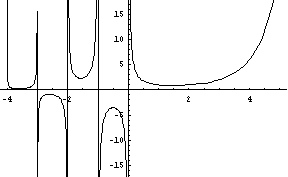
(рис.1)
4. Вычисление некоторых интегралов. 16
Формула Стирлинга
Применим гамма функцию к вычислению интеграла:
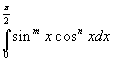
где m > -1,n > -1.Полагая , что
![]() ,имеем
,имеем
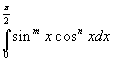
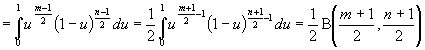
и на основании (2.2) имеем
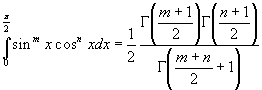 (3.1)
(3.1)
В интеграле
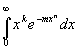
Где k > -1,n > 0,достаточно положить
![]()
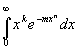
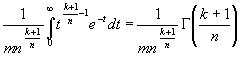
Интеграл
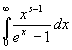
Где s > 0,разложить в ряд
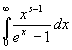
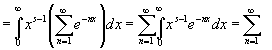
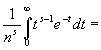
=
![]()
где
![]() дзетта функция Римана
дзетта функция Римана
Рассмотрим неполные гамма функции (функции Прима)
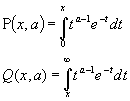
связанные неравенством
![]()
![]()
Разлагая,
![]() в ряд имеем
в ряд имеем
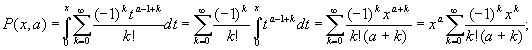
![]()
Переходя к выводу формулы Стирлинга , дающей в частности приближенное значение n! при больших значениях n ,рассмотрим предварительно вспомогательную функцию
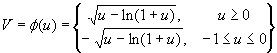 (3.2)
(3.2)
Непрерывна на интервале (-1,
![]() ) монотонно возрастает от
) монотонно возрастает от
![]() до
до
![]() при изменении
при изменении
![]() от
от
![]() до
до
![]() и обращаются в 0 при u = 0.Так как
и обращаются в 0 при u = 0.Так как
![]()
то
![]() при u > 0 и при u < 0 , далее имеем
при u > 0 и при u < 0 , далее имеем
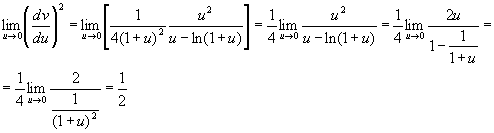
И так производная непрерывна и положительна во всем интервале
![]() ,удовлетворяет условию
,удовлетворяет условию
![]()
Из предыдущего следует, что существует обратная функция,
![]() определенная на интервале
определенная на интервале
![]() непрерывная и монотонно возрастающая в этом интервале,
непрерывная и монотонно возрастающая в этом интервале,
Обращающаяся в 0 при v=0 и удовлетворяющая условие
Формулу Стирлинга выведем из равенства
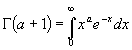
полагая
![]() ,имеем
,имеем
![]()
Положим далее
![]() введенная выше обратная функция, удовлетворяющая условиям u = -1при
введенная выше обратная функция, удовлетворяющая условиям u = -1при
![]() ,и
,и
![]() при
при
![]() .Замечая что(см.3.2)
.Замечая что(см.3.2)
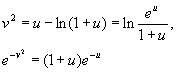
имеем
![]() ,
,
полагая на конец ,
![]() ,получим
,получим
![]()
или
![]()
в пределе при
![]() т.е. при
т.е. при
![]() (см3.3)
(см3.3)
![]()
откуда вытекает формула Стирлинга
![]()
которую можно взять в виде
21
где
![]() ,при
,при
![]()
![]()
для достаточно больших
![]() полагают
полагают
вычисление же производится при помощи логарифмов
![]()
если
![]() целое положительное число, то
целое положительное число, то
![]() и (3.5) превращается в приближенную формулу вычисления факториалов при больших значениях n
и (3.5) превращается в приближенную формулу вычисления факториалов при больших значениях n
![]()
приведем без вывода более точную формулу
![]()
где в скобках стоит не сходящийся ряд.
5. Примеры вычисления интегралов 22
Для вычисления необходимы формулы:
![]()
![]()
Г(
![]() )
)
![]()
Вычислить интегралы
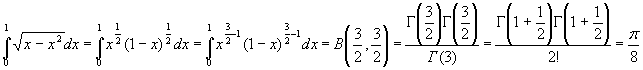
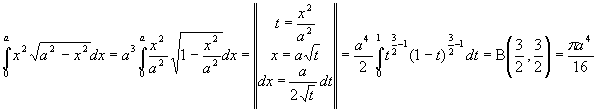
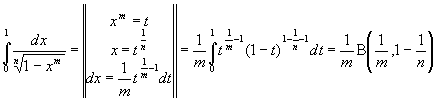
![]()
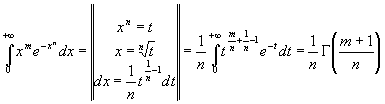
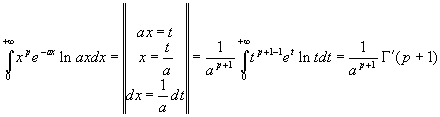
Міністерство освіти і науки України
Запорізький державний університет
ДО ЗАХИСТУ ДОПУЩЕНИЙ
Зав. каф. Математичного аналізу
д. т. н. проф. ____ С.Ф. Шишканова _________________________ 2002р.ПОЯСНЮВАЛЬНА ЗАПИСКА ДО КУРСОВОГО ПРОЕКТУ
ГАМА ФУНКЦІЇ
Розробив
Ст..гр.. 8221-2
Садигов Р.А.Керівник
Ст. викладач
Кудря В.І.
Запоріжжя 2002.
Содержание
Задание на курсовую работу ...................................2
Реферат ...................................4
введение ...................................5
вывод ..................................24
Список литературы……………………………………………..............25
Реферат
Курсовая работа: 24 ст., 5 источников, 1 рис.
Обьект иследований: гамма и ее приложения.
В работе идет речь о представлении бета и гамма функций с помощью интегралов Эйлера соответствено первого и второго рода. И о их применении для вычисления интегралов.
Ключевые слова:
ГАММА И БЕТА ФУНКЦИЯ, ИНТЕГРАЛ ЭЙЛЕРА, ПРОИЗВОДНАЯ, ПРЕДЕЛ.
Введение
Выделяют особый класс функций, представимых в виде собственого либо несобственого интеграла, который зависит не только от формальной переменной, а и от параметра.
Такие функции называются интегралами зависящими от параметра. К их числу относятся гамма и бета функции Эйлера.
Бета функции представимы интегралом Эйлера первого рода:
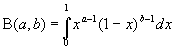
гамма функция представляется интегралом Эйлера второго рода:
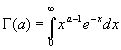
Вывод
Гамма функции являются удобным средством для вычисления некоторых интегралов в частности многих из тех интегралов, которые не представимы в элементарных функциях.
Благодаря этому они широко применяются в математике и ее приложениях, в механике, термодинамике и в других отраслях современной науки.
Список литературы
1. Специальные функции и их приложения:
Лебедев И.И.,М.,Гостехтериоиздат,1953
2. Математический анализ часть 2:
Ильин О.А., Садовничий В.А., Сендов Бл.Х.,М.,”Московский университет”,1987
3. Сборник задач по математическому анализу:
Демидович Б.П.,М.,Наука,1966
4. Интегралы и ряды специальные функции:
Прудников А.П., Брычков Ю.А.,М.,Наука,1983
5. Специальные функции:
Кузнецов , М.,”Высшая школа”,1965