Вопросы к гос.экзамену по дисциплине “Математика – Алгебра”

Вопрос 3. Определитель квадратной матрицы .

В вопросе рассматривается одна из характеристик матрицы - числовая. Все свойства определителя (числовые характеристики) матрицы рассматриваются для того, чтобы это число стало возможным находить. Введение понятия определителя матрицы позволяет расширить возможности теории решения систем линейных уравнении и другие приложения теории матриц.

Итак, введем определение определителя матрицы и рассмотрим его свойства.

Пусть дана квадратная матрица А=(aij)n n, где аij О R

Для введения определения матрицы обратимся к некоторым вопросам теории подстановок.

Подстановка t = 1 2 … n называется взаимно-однозначное

t (1) t (2) …t (n)

отображение множества М={1,2,...,n} на себя. Множество всех подстановок обозначается Sn, |Sn|=n!

Подстановки характеризуются своей четностью и нечетностью, которые вводятся через инверсию:

-если у подстановки четное число инверсии, то она четная;

-если-нечетное число инверсий, то она нечетная.

Для обозначения четности подстановки используется символ sgn(t ) -знак подстановки. Зафиксируем ряд необходимых утверждений:1) t = E (единичная)-четная; 2) sgn (t ^--1 ) = sgn t ;

3) одна транспозиция меняет четность подстановки.

Опр.1. Определителем квадратной матрицы называется число, равное сумме n! слагаемых, каждое из которых есть произведение n элементов матрицы, взятых ровно по одному из каждой строки и каждого столбца матрицы со знаком sgn (t )

где t -подстановка из индексов элементов произведения ,т.е.

|A|=е sgn(t )a _{1t (1)} a _{2t (2)} …a _{nt (n) ,} A=(a _ij ) _n*n

приняты также обозначения для определителя: def A, Δ.

Теорема 2. Определитель матрицы обладает рядом свойств, среди которых следующие:

1 . |A|=|A ^t |,где А ^t -трансионированная;

2 . Определитель матрицы с нулевой строкой равен нулю;

3 . Определитель матрицы с двумя пропорциональными строками равен нулю.

4 . Определитель матрицы с двумя равными строками равен нулю.

5 . Перестановка двух строк(столбцов) матрицы изменяет знак определителя.

6 . Если к одной строке матрицы прибавить другую,уменьшенную на число, не изменяет ее определитель.

7 . Если i-строка (столбец) матрицы имеет вид i(a ₁ +...a _k b1+...b _k c ₁ +....c _k ),то определитель такой матрицы равен сумме K-определителей,каждый из которых в i-строке имеет соответственно ее слагаемые, а остальные элементы совпадают с элементами матрицы.

8 . Если строку (столбец) матрицы умножить на число x, то определитель матрицы умножится на это число.

и другие.

Для решения проблемы вычисления определителя матрицы вводятся понятия минора элемента a _ij (M _ij ) и его алгебраического дополнения (A _ij ) .

Минором M _ij элемента a _ij матрицы называется определитель матрицы, полученный вычеркиванием i-строки и j-столбца.

Алгебраическим дополнением Aij элемента a _ij называется число (-1) ^i+j М _ij

Имеет место теорема о разложении по элементам строки (столбца).

Теорема 3 . |A|= a _1j A _1j +a _2j A _2j +....+a _nj A _nj или

|A|=a _i1 A _i1 +a _i2 A _i2 +...+a _in A _in .

Доказательство разобьем на три случая:

Cлучай 1. a ₁₁ …a _1n

|A|= a ₂₁ …a _2n = a _nn M _nn

0……a _nn

Воспользуемся для доказательства определением определителя

|A|=е sgn(t )a _{1t (1)} a _{2 t (2)} …a _{n-1,t (n-1)} a _{nt (n)}

Так как в n-ой строке все элементы кроме a _nn нули, то все слагаемые в определителе кроме a _nn равны нулю. Тогда определитель такой матрицы равен:

sgn(t ) a _{1t (1)} a _{2 t (2)} ....a _{n-1,t (n-1)} a _{n n} =a _{n n} ( sgn(t ’) a _{1t (1)} a _{2 t (2)} ...a _{n-1,t (n-1)} ),где

t = 1 2 ... n-1 n t ’ = 1 2 ... n-1

t ₍₁₎ t ₍₂₎ ... _{t (n-1)} t _(n) , t ₍₁₎ t ₍₂₎ ... t _(n) , т.к

t = 1 2 ... n-1 n = 1 2 .... n

t ₍₁₎ t ₍₂₎ ... t _(n-1) t _{(n )} t ₍₁₎ t ₍₂₎ ... t _(n) ,то sgn (t ) =sgn(t ’).

Мы видим, что в скобках определитель порядка (n-1),полученного вычеркиванием n-ой строки и n-ого столбца. Поэтому

|A|=a _nn M _nn , что и требовалось доказать.

Случай 2.

a ₁₁ ... a _1j .. a _1n

|A|= ................................. = a _ij A _ij

0 ... a _ij ... 0

..................................

a _n1 ... a _nj ... a _nn

Для доказательства воспользуемся свойством перестановки строк и столбцов матрицы, получим:

A _{11 ...} a _1j ... a _1n a ₁₁ .. a _1j ..a _1n a ₁₁ .. a _1n .. a _1j

A = ....................... = ^n-i .................... = ^n-i ^n-j .................... =

0 .. a _ij ... 0 a _n1 .. a _nj ..a _nn a _n1 .. a _nn ..a _nj

a _{n1 ..} a _nj ... a _nn 0 .. a _ij .. 0 0 .. 0 .. a _ij

= ^2n- M _ij *a _ij = ^i+j a _ij M _ij =a _ij A _ij

Случай 3. |A|=a _1i A _1i +a _2i A _2i +....+a _ni A _ni.

A _{11 ..} a _1j .. a _nn ... a _1j +0+..+0 ... .. a _1j .. .. 0 .. ... 0

A ₂₁ .. a _2j .. a _2n ... 0 +a _2j +..+0 .. .. 0 .. .. a _2j .. ... 0

A = ..................... = ......................... = ......... + .......... +..+ ....... =

a _n1 .. a _nj .. a _nn ... 0+0+..+a _nj ... .. 0 .. .. 0 .. ...a _nj

= a _1j A _1j +a _2j A _2j +..+a _nj A _nj

Рассмотренная теорема позволяет вычислить определитель матрицы любого порядка .Теория определителей имеет приложительное значение, то есть используется в качестве средства для решения вопрос в математике. В частности, она лежит в основе решения систем линейных уравнений как одного из способов. Возможность использования теории определителей для решения систем зафиксированы теоремой Крамера.

Теорема 4. (Крамера). Если |A| не равен нулю, то система е a _ij x _j =b _i , где i=1,n; j=1,n имеет единственное решение, которое находится по формуле:

x _i = , где = A ,

D x _i -определитель матриц, полученных из А заменой i-столбца столбцом свободных членов.

Пусть (1) е a _ij x _j =b _j , i=j=1,n, |A| № 0. Запишем систему (1) в виде матричного уравнения (2): AX=b, где А-основная матрица системы, .

X ₁ b ₁

X= X ₂ , b = b ₂

.. ..

x _n b _n

Если |A| № 0® $ А ^-1 Ю А ^-1 АХ=А ^-1 b Ю X=A ^-1 b. Известна теорема утверждающая, что A ^-1 = A ^* , где A ^* -присоединенная матрица к матрице A, она состоит из алгебраических дополнений элементов, расположенных в столбцах. Тогда:

A ₁₁ A ₂₁ .. A _n1 b ₁ b ₁ A ₁₁ +b ₂ A ₂₂ +..+b _n A _n1

X= A ^* b = A ₁₂ A ₂₂ .. A _n2 b ₂ = b ₁ A ₁₂ +b ₂ A ₂₂ +..+b _n A _n2 =

........................ ... ...................................

A _1n A _2n .. A _nn b _n b ₁ A _1n +b ₂ A _2n +..+b _n A _nn

x ₁

= x ₂ ,

......

x _n

что и позволит получить формулу: X _i = , где = A , i=1,n

Вопрос 4. Бинарные отношения.

Математика как наука отражает мир взаимодействующих простых и сложных объектов (вещей, явлений, процессов). Абстрагируясь от реальности, математика рассматривает унарные, бинарные и другие отношения.

В вопросе требуется рассмотреть бинарные отношения, их свойства и особо обратить внимание на отношение эквивалентности, заданного на одном множестве. Рассмотрим прямое произведение двух множеств. A*B={a,b}, aО A, bО B}. Мы имеем множество упорядоченных пар. Есть смысл рассматривать его подмножество, которое и носит название “бинарное отношение”.

Опр.1 Бинарным отношением, заданным на множестве А, называется подмножество прямого произведения А*А. В силу своей природы, бинарные отношения являются множеством упорядоченных пар элементов из А.

Обозначения: W={ ( a,b) /,a,bО A} ; aWb, a,bО A; ( a,b) О W,где a,bО A

Например, бинарные отношения являются:

1. "^ "на множестве прямых.

2. "=" на множестве чисел.

3. " @ " изоморфизм на множестве алгебр.

4. " ~ " эквивалентность систем и др.

Бинарные отношения могут обладать свойствами:

1) рефлексивность: " aО A, aWa;

2) симметричность: " a,bО A, aWbЮ bWa;

3) транзитивность: " a,b,c О A,aWb и bWcЮ aWc

4) связность: " a,bО A,aWbЮ bWa;

5) антирефлексивность: " aО A,( a,a) П W;

6) антисимметричность: " a,bО A,aWb,bWaЮ a=b

В зависимости от того, каким набором свойств обладают отношения, они допускают

классификацию, которую представим схемой:

Бинарное

отношение

функциональность эквивалентность: порядок:

" xО A, $ ! yО A: рефлексивность, антисимметричность,

f:x® y cимметричность, транзитивность

транзитивность

строгий порядок: нестрогий порядок:

антирефлексивность рефлексивность

частичный порядок: полный порядок:

не обладает свойством обладает связностью

связности

Остановимся на отношении эквивалентости, то есть на отношении WМ A*A, обладающее свойствами рефлексивности, симметричности, транзитивности. Легко проверить, что примерами таких отношений являются "=", "~", "сравнение по модулю", изоморфизм алгебр и другие.

Отношение эквивалентности играет большую роль в математике, значимость его определяется тем, что оно задает разбиение, а потому позволяет получать новые множества. Рассмотрим это подробнее.

Разбиением множества называется совокупность непустых подмножеств, непересекающихся, объединение которых совпадает с данным множеством.

Имеет место теорема, которая позволяет рассматривать отношение эквивалентности как разбиение.

Теорема 2. Бинарное отношение задает на A№ 0 разбиение.

Для доказательства теоремы введем такое понятие как класс эквивалентности:

K _a ={ x/xWa /x,aО A} a-образующий элемент класса.

свойствами рефлексивности, симметричности, транзитивности. Легко проверить, что примерами таких отношений являются "=", "~", "сравнение по модулю", изоморфизм алгебр и другие.

Имеет место теорема, которая позволяет рассматривать отношение эквивалентности как разбиение.

Теорема 2. Бинарное отношение задает на A№ 0 разбиение.

Для доказательства теоремы введем такое понятие как класс эквивалентности:

a-образующий элемент класса.

Классы эквивалентности обладают свойствами:

1. " aО A попадает в какой-либо класс, что означает, что K _{a№ 0} . Это утверждение следует из введенного определения класса.

Любые два элемента из класса находятся в отношении, т.е. если b,cО K _a , b w c.

c,bО K _aЮ a w c, Ю c w a , Ю c w b

a w b a w b

Это свойство позволяет утверждать, что любой представитель класса может являться его образующим.

3° . Классы не пересекаются, т.е. КаЗ Кb=Ж

Пусть КаЗ Кb№ Ж ® $ сО КаЗ КbЮ сО Ка,сО КbЮ сWа,cWbЮ аWс,сWbЮ аWbЮ Ка=Кb.

Свойства классов и позволяют утверждать истинность теоремы: A,W-эквивалентности Ю Ka ,Kb ,...Ю

a) классы-подмножества A;

b) классы-неизвестного подмножества;

c) классы-не пересекающиеся;

d) И Ka =A , аО А

Имеет место и обратное утверждение.

Теорема 3. Если на А задано отношение Rs, соответствующее разбиению S, то Rs-отношение эквивалентности .

Пусть A, Rs, S-разбиения, следовательно, A разбивается на подмножества, объединение которых составляет A.

Если подмножества рассматривать как классы, полученные в результате отношения Rs: "принадлежность одному подмножеству", то легко доказать, что все свойства классов имеют место, поэтому Rs-эквивалентность.

Обозначим множество классов эквивалентности через A/w. Это новое множество называют фактор-множеством . Итак, A/w= { Ka /a О A } .

Рассмотрим некоторые примеры применения теории отношении эквивалентности:

Hа множестве дробей {a/b, аО Z, bО N} зададим отношение "=": а/b=с/dЫ ad=bс.

Тогда класс эквивалентности Ка/b={x/y| x/y=a/b}-рациональное число, а {Ka/b}=A/W-множество рациональных чисел.

2. Z, “є ”: aє b(mod m)Ы (a-b)M m, {Ka}=Z/(m)=Zm-основное множество кольца классов вычетов.

3. Ф-множество фигур, " ~ "-подобие. Это отношение рождает понятие "форма фигуры" как класса подобных фигур.

Вопрос 5 . Элементы теории групп .

Алгебра как наука изучает различные алгебры: векторные пространства, группы, кольца. В вопросе требуется рассмотреть одну из них – группу. Определение группы задается аксиометрически и рассматривается одно из наиболее важных отношений, которое изучает эта наука, отношение эквивалентности, которое позволяет получать новые группы. Введем понятие алгебры.

Опр. 1. Алгеброй называется упорядоченная пара множеств <A,V>,где A-множество элементов любой природы, а V-множество алгебраических операций.

Опр. 2. Пусть дано множество A№ Ж . Алгебраическая операция “o ” на множестве А называется отображение f: А® А, т.е. для " a,bО A, ($ ! ) cО A:ao b=c

Опр. 3. Группой называется алгебра <G, o > с одной алгебраической операцией “ o ”,

удовлетворяющей свойствам (аксиомам):

1° ." a,b,cО G, ao (bo c)=(ao b)o c,

2° .$ eG," aО G: eo a=ao e=a.

3° ." aО G, $ a° О G:ao a° =a° o a=e.

e-нейтральный элемент относительно операции;

а° -симметричный относительно операции для а.

Группа, как алгебра, обладающая рядом свойств допускает классификацию.

Будем рассматривать дальнейшие теоретические вопросы в терминах мультипликативной группы.

Теорема 4 (свойства группы). В группе нейтральный элемент единственный, для каждого элемента обращение единственно, уравнения ax=b, xa=b разрешимы и имеют единственное решение.

1. Пусть для еО G, $ e ₁ ,e ₂ -нейтральный (единственный), рассмотрим

(1):e ₁ e=ee ₁ =e.

(2): e ₂ e=ee ₂ , откуда получим:

e ₁ =e ₁ e=e ₁ ee ₂ =ee ₂ =e ₂ , т.е. e ₁ =e _2.

2. Пусть для aО G, $ a ₁ ^-1 , a ₂ ^-1 -обратный для а.

Рассмотрим (1): a ₁ ^-1 a=aa ₁ ^-1 =e

(2): a ₂ ^-1 a=aa ₂ ^-1 =e , откуда получим:

a ₁ ^-1 aa ₂ ^-1 =ea ₂ ^-1 =a ₂ ^-1 ,

a ₁ ^-1 aa ₂ ^-1 =a ₁ ^-1 e=a ₁ ^-1 Ю a ₂ ^-1 =a ₁ ^-1 .

3. ax=b; aО GЮ $ a ^-1 : aa ^-1 =a ^-1 a=e. Домножим уравнение на a ^-1 :

a ^-1 ax=a ^-1 bЮ ex=a ^-1 bЮ x=a ^-1 b.

Пусть уравнение имеет два решения x ₁ , x ₂ :

ax ₁ =b, ax ₂ =b-равенства, домножим на а ^-1 :

x ₁ =a ^-1 b, x ₂ =a ^-1 b.

В силу алгебраичности операции x ₁ =x ₂ , что и требовалось доказать.

Из определения группы видно, что G это множество, поэтому есть смысл рассматривать его подмножества. Среди подмножеств особый интерес представляют те, которые являются группами, т. е. замкнуты относительно той же групповой операции.

Опр. 5. Подмножество К группы <G, * > называется подгруппой, если оно само является группой <K, * > .

Теорема 6. (критерий подгруппы). Подмножество К группы G является подгруппой тогда и только тогда, когда выполнены два условия:

1° ." a,bО K, ab,baО K.

2° ." aО K, a ^-1О K.

Ю G-группа, K М G. Пусть K p G (подруппы), тогда по определению К-группа. Следовательно, 1° ,2° выполнены.

Ь G-группа, K М G, 1° , 2° . Покажем, что K p G, т. е. К-группа.

Для доказательства необходимо проверить четыре условия:

Замкнутость К относительно групповой операции.

Ассоциативность этой операции.

Существование нейтрального элемента.

Существование для каждого элемента обратного.

Из условия видно, что 1 и 4 выполнены. Второе имеет место в силу того, что КМ G. Проверим 3:

Т. к. " aО K, $ a ^-1О K ,условие 1° , то аa ^-1 О К. Но аa ^-1 = е, следовательно, еО К, что и требовалось доказать. Критерий важен в теории групп тем, что сокращает процедуру проверки, является ли подмножество группой (подгруппой).

Особую роль в теории групп имеют подгруппы, называемые нормальными, или нормальными делителями. Выведем это понятие.

Пусть G-группа, K p G-подгруппа. Зададим отношение “сравнения по подгруппе К”:

aє b(mod K)Ы ab ^{-1 О} K. Проверим, что отношение “є ”-является эквивалентностью.

1).]aО GЮ $ a ^-1 G, aa ^-1 =e, eО KЮ aa ^-1О KЮ aє a(mod K)Ю ”є ”-рефлексивно.

2).]aє b(mod K)Ю ab ^-1О K, (a-b ^-1 ) ^-1О KЮ ba ^-1О KЮ bє a(mod K)Ю ”є ”-симметрично.

3).]aє b(mod K), bє c(mod K)Ю ab ^-1О K, bc ^-1О KЮ (ab ^-1 )(bc ^-1 )О KЮ ac ^-1О KЮ

aє c(mod K)Ю ”є ”-транзитивно.

Таким образом, отношение сравнение по модулю в G является отношением эквивалентности, а эквивалентность, как известно, задает разбиение на G.

Обозначим класс эквивалентности, образованный элементами g О G, gЇ и покажем, что gЇ=Kg={hg| hО K, gО G}

Тогда множество классов эквивалентности, которые называются смежными классами группы G по подгруппе К, образуют фактор-множество.

{Kg| gО G}=G/”є ”-фактор-множество.

Аналогично можно вывести отношение сравнения по подгруппе иначе:

“aє b(mod K)Ы b ^-1 aО K”.

Для различения классы Кg и gК называют правым и левым, причем И Кg=G и И gK=G, a {Kg/gО G} и {gK/gО G}-образуют фактор-множества.

Возможен случай, когда для " gО G, Kg=gK. В этом случае К обозначают буквой Н и называют нормальным делителем группы G по Н. Чем интересен этот случай? Оказывается, над смежным классом группы G по Н можно производить операции, а это позволяет рассматривать новую алгебру.

Зададим операцию “ * ” на множестве смежных классов {Hg/g}, где нормальная подгруппа группы G так: Hg ₁ Hg ₂ =Hg ₁ g ₂ . Покажем, что выведенная таким образом операция является алгебраической, т. е. покажем, что умножение не зависит от представителей классов, т. е., если

a, a'О Hg ₁ , b,b'О Hg ₂ , то abє a'b'(mod H), т.е. ab, a'b'О Hg ₁ g _2.

ab=(h ₁ g ₁ )(h ₂ g ₂ )=h ₁ h ₂ g ₁ g ₂ =hg ₁ g _2Ю abО Hg ₁ g ₂ ;

a'b'=(h ₁ 'g ₁ )(h ₂ 'g ₂ )=h ₁ 'h ₂ 'g1g2=h'g ₁ g _2Ю a'b'О Hg ₁ g ₂ , следовательно

ab, a'b' принадлежит одному классу, т. е. Операция “ * ” на множестве классов является алгебраической, что и дает возможность рассматривать новую группу.

Теорема 7. Множество смежных классов группы G по нормальной подгруппе Н образуют группу.

Т. к. G, H p G-нормальная, {Hg/g G}=G/”є ” . Зададим операцию: Hg ₁ Hg ₂ =Hg ₁ g ₂ . Покажем, что фактор-множество по введенной операции является группой.

1° .Hg ₁ (Hg ₂ Hg ₃ )=Hg ₁ (Hg ₂ g ₃ )=Hg ₁ (g ₂ g ₃ )=H(g ₁ g ₂ )g ₃ =Hg ₁ g ₂ Hg ₃ =(Hg ₁ Hg ₂ )Hg _3Ю операция ассоциативная.

2. Hg=He=H " Hg, H: HgH=HgHe=Hge=Hg, т. е. Н-выполняет роль нейтрального элемента на фактор-множестве.

3.Hg, Hg ^-1 : HgHg ^-1 =Hgg ^-1 =He=H;

Hg ^-1 Hg=Hg ^-1 g=He=H, семейство класса Hg ^-1 выполняет роль обратного для Hg,

т.е. (Hg) ^-1 =Hg ^-1 .

так как все аксиомы имеют место, то мы имеем дело с группой. Ее обозначают G/H и называют фактор-группой.

Вопрос 6 Элементы теории колец.

В вопросе требуется ввести понятие кольца, рассмотреть классификацию колец и построить фактор-кольцо.

Так как кольцо это пример одной из алгебр, то следует напомнить определение алгебры.

Опр.1

Алгеброй называется упорядоченное множество двух множеств <A,U>, где А 0

множество элементов любой природы, а U-множество операций.

Для введения определения кольца необходимо рассмотреть непустое множество и задание операций.

Опр.2

Кольцом называется алгебра < K,+, > с двумя бинарными операциями, которые

удовлетворяют следующим свойствам:

1. < K, +> - аддитивная абелева группа,

2. “ ,, - ассоциативно,

Имеет место два дистрибутивных закона, то есть а,в,с

К , а(в+с)=ва+са.

Кольцо как алгебра допускает классификацию, представим её схемой:

Кольцо

С единицей, т.е.		Без единицы


Коммутативны т.е.		Не коммутативны

С делителями нуля, т.е.

Без делителей

нуля.

Замечание: Определение всех классов колец предоставляется сформулировать читателю.

Опр.3

Коммутативное кольцо с единицей без делителей нуля называеться областью

целостности.

Примером области челосности является кольцо Z , колцо многочленов от одной переменной K , где К- область челостности.

Так как кольцо это алгебра, а алгебра это множество, то есть смысл говорить о его

подмножествах, среди которых особый интерес представляют подкольца.

Опр.4

Подмножество I кольца К называется его подкольцом, если оно само является

кольцом относительно операции кольца К .

Для проверки является ли рассматриваемое подмножество кольца К его подкольцом удобно пользоваться критерием подкольца.

Теорема 5.

(критерий подкольца) Подмножество I кольца К является подкольцом

тогда и только тогда, когда оно замкнуто относительно вычитания элементов и умножения , т.е. если (1)

(2)

Ь Пусть (где “

,,- “ быть подкольцом ,,) .Покажем что (1) и (2) имеют место.

Так как , то он является кольцом, а кольцо это абелева група, тогда для , поэтому следовательно (1) выполнено. Выполнимость (2) вытекает из того что I замкнуто относительно умножения.

Пусть

, (1),(2) – выполнены. Покажем, что I – подкольцо, т.е. что I – кольцо.

Для этого проверим выполнимость всех аксиом кольца. Из (2) следует, что I – замкнуто относительно умножения, ассоциативность умножения следует из того,что .

Рассмотрим условие (1). Пусть ,но , , ассоциатив -ность сложения вытекает из того что . Таким образом, все аксиомы кольца имеют место в I , следовательно, I – кольцо. Так как , то это подкольцо.

Интересен случай подкольца, когда оно является идеалом. Введём это понятие.

Опр. 6

Подкольцо I кольца K называется идеалом если для

В кольце с существует особый идеал: Такой идеал называется главным идеалом. Главный идеал является наименьшим подкольцом, образованным

Пусть К является областью целостности. Зададим на нём отношение “сравнения по идеалу I ”.

Опр.7

. Легко проверить, что “ “ – отношение эквивалентности:

1 ⁰ .т.к .а-а=0О I, то отношение рефлексивно

2 ⁰ . Если а є в( mod I) Ю а-вО I Ю в-аО I Ю в є а( mod I) Ю отношение симметрично

3 ⁰ .Если а є в( mod I) , в є c( mod I) Ю а-вО I, в-сО I Ю (а-в)+(в-с)= а-сО I Ю

а є c( mod I) Ю отношение транзитивно.

Как известно, отношение эквивалентности задаёт разбиение.

К _а - класс эквивалентности по отношению сравнения по идеалу, называется классом вычетов. Классы вычетов обладают всеми свойствами классов эквивалентности, т.е.

классы эквивалентности не пустые,

классы не пересекаются,

классы состоят из элементов кольца, связанные заданным отношением

каждый элемент из K входит в один из классов

объединение классов вычетов совпадает с кольцом.

Множество классов вычетов { К _а /а К } называется фактор-множество.

Имеет место теорема о фактор-множестве.

Теорема 8

Фактор-множество с операциями сложения и умножения классов вычетов

является кольцом.

Для доказательства выполним следующие процедуры:

зададим операции и проверим их корректность;

операции подчиняются аксиоматике кольца.

n 1). К _а +К _в =К _а+в , К _а К _в =К _ав

К _а , К _в покажем, что а+в

К _а , а+в К _а+в , К _в

ав

Покажем, что К _{а+в ,} К _ав

Если и

_а+в

_ав

что доказывает, что введённые операции корректны, т.е. являются алгебраическими.

2). К _а +(К _в +К _с )=К _а +К _в+с =К _а+(в+с) =К _(а+в)+с =К _(а+в) +К _с =(К _а +К _в )+К _с сложение ссоциативно

К _а +К _в =К _а+в =К _в+а =К _в +К _а сложение коммутативно;

К _а +К ₀ =К _а+0 =К _а К ₀ =I идеал выполняет роль нулевого элемента относительно сложения;

К _а +К _(-а) = К _а+(-а) = К ₀ = I К _(-а) = -К _а –противоположные классы

К _а ^. (К _в ^. К _с ) = К _а ^. К _вс =К _а(вс) =К _(ав)с =К _ав ^. К _с = (К _а ^. К _в ) ^. К _с

К _а ^. (К _в +К _с ) = К _а К _в+с = К _а(в+с) = К _ав+ас = К _ав +К _ас

Всё рассмотренное доказывает выполнимость аксиоматики кольца, поэтому - кольцо. Оно обозначается и называется фактор-кольцом кольца К по идеалу I .

Кроме отношения сравнения по идеалу I в кольце рассматривается ещё отношение-

“ отношение делимости “. Рассмотрим его.

Опр. 7

Элемент называется делящимся на элемент в кольце К, если существует

такое , что а=вс. а – называется делимое, в –делитель, с –частное. И обозначается “ M ,,

Отношение делимости позволит ввести ещё одно отношение – ассоциативности элементов - “ ~ ,, а ~в аM в / вM а.

Элемент называется обратимым в К если для него существует такое, что

ав =1. Элементы а и в называют так же делителями единицы.

Отношение делимости обладает рядом свойств, оно является нестрогим числовым порядком, т.е.

1 ⁰ “ M ,, - рефлексивно : а 0, аM а.

2 ⁰ “ M ,, - антисимметрично : аM в, вM а Ю а = в.

3 ⁰ “ M ,, - транзитивно : аM в, вM с, то аM с.

4 ⁰ а,вM с Ю а+вM с, авM с.

5 ⁰ а ₁ ,а ₂ , .... ,а _n , a _I M c Ю а ₁ ,а ₂ , ... ,а _{n M} с . и ряд других свойств.

Отношение “ ~ “ является отношением эквивалентности.

1 ⁰ M а Ю а ~ а.

2 ⁰ а ~в Ю аM в, вM аЮ в ~а.

3 ⁰ а ~в, в~с Ю аM в, вM с Ю аM с _Ю c~a Ю a ~c

вM a, сM в Ю сM в ,в M а Ю сM а

Вопрос 7 Гомоморфизм колец

В вопросе ставиться проблема взаимосвязи алгебр на примере колец, которые описываются гомоморфизмом. Предлогаеться решить проблему взаимосвязи кольца, фактор-кольца с другим кольцом, которая задаётся теоремой об эпиморфизме колец. Предварительно введём ряд понятий. Прежде всего, сформулируем определение алгебры и гомоморфизма алгебры.

Опр.1

Алгеброй называется упорядоченное множество двух множеств <A,U>, где А 0

множество элементов любой природы, а U-множество операций.

Для введения определения кольца необходимо рассмотреть непустое множество и задание операций.

Опр.2

Гомоморфизмом алгебр называется отображение одной из них в другое, сохра -

няющее операции, т.е. если А , В – алгебры , с U, W – множествами опреаций, f – гомоморфизм А в В , то ▲ U, существует ■ W.

Гомоморфизм алгебр допускает классификацию:

Свойства f	Гомоморфизм	Мономорфизм	Эпиморфизм	Изоморфизм
1.Сохранение операций
2.x ₁ y _1Ю f (x ₁ ) f (y ₁ )

Все св-ва 1 - 3

Сформулировать определения мономорфизма, эпиморфизма, изоморфизма предоставляется читателю.

Рассмотрим гомоморфизм колец.

Опр.3

Гомоморфизмом кольца <K, +, > в < > называют отображение f :

Сохраняющее операции, т.е. f(а+в)=f(а)Е f(в) ; f(ав)=f(а)Д f(в).

Опр.4

Ядром гомоморфизма f : называется множество элементов из К, образы

которых равны нулю кольца К, т.е. Ker f =

Теорема 5

Ker f кольца К в является идеалом К

а,в О Ker f Ю f(a)=0ў О Kў , f(в)=0ў О Kў ; кО K

f(a-в)=f(а+(-в))=f(а)+f(-в)=f(а)-f(в)=0ў - 0ў =0ў О K Ю а-в О Ker f

f(ак)=f(а) f(к)=0ў f(к)=0ў О Кў Ю акО Ker f

f(ка)=f(к) f(а)= f(к) 0ў =0ў О Кў Ю каО Ker f , что и доказывает, что Ker f кольцо К в К ў является идеалом К

Имея К и идеал его I , можно задать отношение сравнения по идеалу. Известно, что это отношение является эквивалентностью поэтому задано разбиение, а следовательно, фоктор - кольца. Рассмотрим отображение Е : К® К /I, где Е(x)=K _x

Покажем что Е – гомоморфизм ( эпиморфизм ).

E(x+y)=K _x+y =K _x +K _y =E(x)+E(y); E(xy)=K _xy =K _x K _y =E(x)E(y).

" K _x О K / I ;$ xО K, E(x)=K _{x .} Это позволяет утверждать что Е - эпиморфизм _.

Теорема 6

Если f: K® Kў эпиморфизм, то существует изоморфизм K / Ker f на Kў такой,

что эпиморфизм f равен композиции Е и изоморфизма.

Для доказательства теоремы предварительно рассмотрим и зафиксируем условие теоремы.

К, Кў - кольца , f: K® Kў , f(x)=xў -эпиморфизм, тогда f обладает ядром Ker f , которое является идеалом K . Становиться возможным К фиксировать по Ker f = I , получаем фактор –кольцо К / Ker f. Рассмотрим Е: К® Ker f , где E(x)=Kx –эпиморфизм. Теперь можно приступать к доказательству теоремы, которое предполагает выполнение процедур по плану:

покажем что для x,yО K _x , f (x)= f (y),

зададим отображение Y : K /Ker f ® Kў так :Y ( K _x )= f (x),

проверим, что Y - гомоморфизм,

Y - эпиморфизм,

Y - мономорфизм.

f = Y ° E .

Итак, покажем, что для x,yО K _x , f (x)= f (y). Пусть f (x)№ f (y) Ю f (x)- f (y)№ 0ў Ю f (x-y)№ 0ў ® x-y П Ker f Ю x y(mod Ker f )Ю xП K _x Ъ yП K _y ,что противоречит условию. Поэтому утверждение верно. Изобразим условие теоремы и результат доказанного схемой

· x f f(x) Kў

· y

Ker f 0ў

E Kx

0ў ў K¤ Ker f

Зададим отображение Y : К/ker f® K’ , Y (Kx)=f(x).

Y (Kx+Ky)=Y (Kx+y)=f(x+y)=f(x)+f(y)=Y (Kx)+Y (Ky);

Y (KxKy)=Y (Kxy)=f(xy)=f(x)f(y)=Y (Kx)Y (Ky), т. е. Y -гомоморфизм.

Кх№ КуЮ Y (Кх)№ Y (Ку).Пусть это не так, пусть Y (Кх)=Y (Ку)Ю f(х)=f(у)Ю х и у из одного класса,что противоречит условию; т.е.Y - мономорфизм. хў О Кў ; т.к. f- эпиморфизм, то$ хО К, f(х)=хў , тогда $ Кх О К(ker f : E(х)=Кх, а Y (Кх)=хў , что позволяет утвердждать: Y - эпиморфизм

Итак , Y -изоморфизм К/ker f и Кў .

Пусть Y оЕ(х) ;Y оЕ(х)=Y (Е(х))=Y (Кх)=f(х)Ю Y оЕ=f

Вопрос 8 . Делимость в кольце целых чисел (Z )

В вопросе ставится проблема отношения делимости в кольце целых чисел и возможное его приложение для нахождения НОД и НОК целых чисел.

Опр.1.

Число а О Z называется делящимся на число в№ оО Z , если существует такое число с, что а=вс,

а называют в этом случае делимым, в – делителем, с – частным. Обозначают отношение І ”.

Отношение делимости на Z обладает рядом свойств:

1° " а№ 0, аM а, | Доказательство:

2° " а№ 0, в№ 0, а:M в, вM аЮ а=в, | а№ 0 Ю а=аЧ 1Ю аM а;

3° " а,в,с, а:в и вM сЮ аM с | аM вЮ а=вс

Истинность названных трех | вM аЮ в=аd } Ю а=а(dс)Ю аЧ 1=а(dс)Ю

Свойств позволяют утверждать, | а(1-dс)=0Ю 1-dс=0Ю dс=1 (нет делителей редко)Ю

Что отношение делимости |d и с делением 1, т.е.равны 1 или (-1)

является нестрогим частичным | аM вЮ а=вк } Ю а=с(mк)Ю аM с

порядком. | вM сЮ в=сm}

4° а:в ,сM вЮ а+вM с, авM с

5° асM вс, с№ 0Ю аM в и ряд других

Убедимся в том, что отношение делимости не обладает свойством связности , т.е. является частичным. Это легко проверить примером: 4: /5. Потому естественным образом возникает проблема деления целого числа на другое не равное нулю. Такая ситуация описывается теоремой о делении с остатком.

Т 2.

" а,в№ 0, Z (!)gч такие, что а=вg+ч, где 0Ј ч< в

Теорема содержит в себе две: о существовании и о единств.

Рассмотрим ихдоказательства.

Случай 1. аі 0.Проведем доказательство методом матиндукции.

а=0 Ю 0=в0+0, где видно , что g=0, r=0О Z

а=п Ю и пусть теорема для п верна, т.е.

(1) п=вg+r, 0Ј r , 0< в

а=п+1Ю прибавим к обеим частям равенства (1) по 1, получим:

п+1=вg+(r+1). Исследуем (r+1).Если r+1< в, то теорема верна для п+1, если r+1=в,то

п+1=в(g+1)+0 и теорема вновь верна. На основании принципа матиндукции можно утверждать,что теорема верна для любого целого числа аі 0.

Случай 2. а< 0, тогда -а> 0 и теорема для этого числа верна, т.е.-а=вg+r 0Ю r< в.

Поступим так:

А=в(-g)+(-r), прибавим к левой части и вычтем в, получим а=в(-g)-в+в+(-r)Ю a=b(-1-g)+

(b-r), где –1-gО Z , в-r < в, при r> 0, т.е. теорема верна.

(!) Пусть для а,в> 0О Z существует два варианта:

а=вg1+r1, а=вg2+r2, где 0Ј r1,r2< в.

Заметим, что g1=g2Ы r1=r2.

Действительно, если r1=r2Ю r1-r2=в(g2-g1)=0, в№ 0Ю g2-g1=0Ю

G1=g2, g1=g2Ю g2-g1=0Ю r1-r2=0Ю r1=r2.

Поэтому рассмотрим случай, когда r1№ r2, тогда вg1+r1=вg2+r2Ю r1-r2=в(g2-g1).

Так как 0 Ј rЈ b, 0Ј r2< b, то r1-r2< b. С другой стороны к b(g2-g1)к = к bк к g2-g1к > g1№ g2> b,

Т.е. R1-r2> b, что привело к противоречнию. Теорема доказана.

Рассмотрим возможное применение отношения делимости и отношения с остатком для введения

и способа вычисления НОД и НОК двух целых (натуральных) чисел. Введем определение

НОД и НОК.

Опр.3 Наибольшим общим делителем двух целых чисел а и в называется такой

Их общий делитель, который делится на всякий другой их общий делитель.

Опр.4. Наименьшим общим кратным двух целых чисел называется такое их

общее кратное , на которое делится всякое другое их общее кратное.

НОД и НОК двух чисел и большего числа можно находить способом разложения на

простые множители. Здесь рассмотрим другие способы в частности, алгоритм

Евклида.

Алгоритм Евклида представляет собой конечный процесс деления одного числа

на другое, затем второго числа на первый остаток, затем первый остаток

деления на второй и так до тех пор, пока деление завершится без остатков.

Это считается возможным, потому что остатки будут неотрицательным числом,

убывают, что бесконечным быть не может.

Оформим этот процесс математически:

а= bg1+r1, 0< r1< b,

b=r1g2+r2, 0 < r2< r1,

…………..

rk-2=rk-1gk+rk, 0< rk< rk-1

rk-1=rkgk+1 rk+1=0

и докажем теорему о нахождении НОД чисел. Заметим, что НОД чисел обозначаем так:

НОД (а;в), или просто (а,в)

Теорема 5

Последний, отличный от нуля, остаток в алгебре Евклида является НОД (а;в).

Для доказательства требуется предварительно рассмотреть две леммы:

Лемма 1: а=вg+r, то (а,в)=(в,r)

(a,b)=d® aM d1bM dЮ a-bgM dЮ rM dЮ d – общий делитель в и r,

т.е., если (в,r)=d1,то d1M d (1)

(в,r)=d1® bM d1, rM d1Ю aM d1Ю d1общий делитель a и b,Ю dM d1 (2)

Из (1) и (2) следует, что d=d1

Лемма 2: аM вЮ (а,в)=в

Теперь допишем теорему. Из последнего равенства в алгоритме Евклида следует, что

(rk-1,rk)=rk. А из предпоследнего, по лемме, следует, что (rk-2,rk-1)=(rk-1,rk)=rk

Поднимаясь от равенства к равенству в алгоритме Евклида получим (а,в)=,rk

Что и требовалось доказать.

Решим вопрос о нахождении НОК (а,в).Обозначим НОК (а,в)=m

И докажем теорему

Теорема 6 m=ab/(a,d). Для доказетельства воспользуемся определением НОК.

Напишем, что ав/(а,в) делится на а и на в.

(а,в)=Ю a=a1d, тогда ab/(ab)=a1db1d/d(a1b1)=ab1=a1b, что и доказывает утверждение.

………..b=b1d

………..(a1,b1)=1

Покажем, что любое кратное чисел а и в делится на m.Пусть М общее кратное а и вЮ

М=ак, М=вmЮ M=abs=absd/d=ab/(a,b)sdЮ

M:ab/(a,b), что и требовалось доказать. Используя определение НОК (а,в) можно

Сделать вывод, что m=ab/(a1b)

Вопрос 9 Элементы теории сравнения с кольце Z

В вопросе решается проблемы возможности задания бинарного отношения

”cравнение по модулю m” в кольце целых чисел, его свойств, среди которых построение

новых алгебр из Z .

Пусть Z -кольцо целых чисел, m О Z , m > 1

Опр.1 Числа а и в называются сравнимыми по модулю m, если а-в:m.

Записывается: а=в(modm).

Легко показать, что введенное бинарное отношение на Z является отношением эквивалентности, т.е.

обладает свойствами рефлексивности ,симметричности ,транзитивности.

Действительно:

1° a-a=0О Z , 0:mЮ aє a (modm);

2° aє b (modm)Ю a-b:mЮ b-a:mЮ bє a (modm);

3° aє b (modm), bє c (modm)Ю a-b:m,Ю (a-b)+(b-c):mЮ a-c:mЮ

…………………………………aє c (modm)

Это очень важное свойство отношения сравнения,т.к. в таком случае оно задает разбиение

На Z , что рождает фактор – множество К/m=Z m, как множество классов эквивалентности.

Общая теория колец рассматривает эту ситуацию и утверждает, что<Z m,+,x> - кольцо.

Здесь же мы рассмотрим порождение другой алгебры – мультипликативной группы.

Для этого введем понятие взаимной простоты класса и модулем m.

Класс Ка=а называется взаимнопростым с m, если (а,m)=1, где а –образующей класса Ка

Однако в теории классов известно, что таким обьразующим может быть любой элемент из этого

класса).

Рассмотрим множество классов вычетов, каждый из которых взаимно прост с m.

Известно, что количество чисел, взаимно простых с модулем определяет функцию

Эйлера g(m) ,и что остатком от деления целых чисел на m составляют полную систему вычетов

Взаимно простые с m следует искать среди классов Ко,К1,К2,…,Кm-1. Пусть такими

классами будут н r1,r2,…rg(m) э . Такую систему классов называют приведенной

Системой классов вычетов и их представителем приведенной системы вычестов

н r1,r2,…rg(m)э .

В этой системе ровно g(m) элементов, ( ri,m)=1, (ri,m)=1

Теперь докажем теорему о приведенной системе классов вычетов.

Теорема 2. Приведенная система классов вычетов по модулю не образует

мультипликативную группу.

Для доказательства теоремы необходимо проверить существенные признаки мультипликативной группы,

т.е. проверить:

замкнутость относительного умножения,

ассоциативность умножения,

существование единичного элемента,

существование для каждого элемента обратного.

Рассмотрим { r1,ri,…rg(m)} ,где (ri,m)=1, напомним ,что riЧ rj=riЧ rj.

(rim)=1Ю

(rj,m)=1

(ri,m)=1

……(rj,m)=1 Если предположить, что (riЧ rj,m)№ 1, то это будет означать, что

най р-простое число такое, что riЧ rj:p1Ю m:p

Если ri или rj делятся на р, то нарушаем условие (1).Если ri p, то по известному утверждению,

І aЧ b:p,(a,p)=1Ю b:pІ , следует, ri:p, что также приводит к противоречию (1). И так,

(ri:rj,p)=1Ю

(riЧ rj,p)=1, т.е.rirgО { r1,r2,…rj(m)} , что утверждает с необходимостью замкнутость

очередного умножения. Так как классы вычетов riО Z m, то умножение

Так как (1,m)=1, то ri=1, т.е. единый класс в рассматриваемом множестве есть.

Пусть аО Z , (а,m)=1, рассмотрим{ ar1,ar2,…arg(m)} .Легко показать, что

Это тоже приведенная система вычетов.Тогда ari=1Ю aЧ ri=1, т.е. для ri

Существует класс ему обратный: а=ri-1. Можно существование обратного класса доказать и таким

Способом: a,r2…rg(m)=rj, сократим на ri, получим r1,r2…rj-1,rj+1 rg(m)=1, тогда

(r2…rg(m)=(r1)-1,(r1r3…rg(m)=(r2)-2 и т.д., что подвтерждает факт существования для

каждого класса ri ему обращенного ri-1. Теорема доказана.

Теория сравнения имеет всевозможное применение. В частности, теория сравнения

Используется при выводе признаков делимости. Сформулируем общий признак

Делимости на mО Z , m> 1, который назван признаком Паскаля. В основе этого признака лежит систематическая запись натурального числа в системе с основанием g, т.е.

(a _n a _n-1 …a ₁ a ₀ )g=a _nЧ g ⁿ +a _n-1 g ^n-1 +…a ₁ g ¹ +a0 _g° .

Теорема 3.(Паскаля) Число а=(а _n ,a _n-1 …a1,a0)g делится на mО Z ,m> 1 тогда и только

Тогда, когда на m деления в число: a _n r _m +a _n-1 r _n-1 +…a ₁ r ₁ +a ₀ r ₀ , где r _i остаток

От деления g _i на m.

g° =mg ⁰ +r ₀ , g ¹ =mg ² +r ₁ ,…g ⁿ =mg ⁿ =r _nЮ

g ^0є r ₀ (m ₀ d _m ),g1є r ₁ (m ₀ d ₀ ),…,g ^nє rn(m ₀ d ₀ ). Используя свойства сравнения легко получаем,

что a _n g ⁿ +…+a ₀ g ^0є a _n r _n +…+a ₀ r ₀ (m ₀ d ₀ ). Воспользуемся определение сравнения, мы получаем истинность теоремы.

Общий признак позволяет вывести частный признак.

Выведем признак делимости на 3 и на 5, если число записано в десятичной

Системе исчисления.

m=3, g=10,тогда 10° =1є 1(mod3),

10є 1 (mod3), используем лемму, можно утверждать, что остатки r _i =1, по

по признаку Паскаля

(a _n a _n-1 …a ₀ )10є a _n +…a ₀ (mod3), откуда можно сфоормулировать признак

делимости на 3:

“Число делится на 3 тогда и только тогда, когла сумма его цифр в

десятичной делится на 3”.

Пусть b О Р(a ), т.к. Р(a ) = Р[ a ] , то b = а _Sa ^s +···+a _1a + a ₀ , где f(х) = а _S х ^s +···+a ₁ х + a _0О Р[ х] , f(a ) = b . Пусть g(х) – линейный элемент для a , т.е. g(х) = b _n х ⁿ + ···+ b ₁ х + b ₀ . Разделим f(х) на g(х) :

f(х) = g(х) g ₁ (х) + r(х), 0Ј deg r(х) < n, т.е. r(х) = с ₀ + с ₁ х +···+ с _n-1 х ^n-1 . (с _iО р).

положим х = a в (1), получим f(a ) = g(a ) g ₁ (a ) + r(a ), т.к. g(a ) = 0, то f(a ) = r(a ), т.е. b = с ₀ + с _1a +···+ с _n-1a ^n-1 . Получили, что такое представление однозначное.

Пусть b = с ₀ + с _1a +···+ с _n-1a ^n-1 и b = d ₀ + d _1a +···+ d _n-1a ^n-1 .

Рассмотрим многочлен φ(х) = (с ₀ - d ₀ ) + (с ₁ - d ₁ )х + ∙∙∙ + (с _n-1 - d _n-1 )х ^n-1 , причем φ(a ) = 0, т.е. получился многочлен, степени меньше чем n, для которого a является корнем, что противеречит линейности многочлена для a . Если φ(х) существует, то он нулевой, поэтому с _i = d _i , что и доказывает теорему.

Посмотрим как возможно изменить эту теорему для освобождения от алгебраической иррациональности в знаменатели дроби.

Пусть a – алгебраический элемент степени n > 1 не из Р

Пусть f(х), h(х) два многочлена из Р[ х] , h(a ) № 0. Тогда в р(a ) может быть дробь . Возникает проблема представить дробь в виде линейной комбинации

степеней a . Это возможно, так как любой элемент из р(a ) есть линейная комбинация 1, a ,…,a ^n-1 Задача состоит в нахождении алгоритма преобразования.

Пусть g(х) – минимальный многочлен для a степени n. Т.к. h(a ) № 0, то h(х) g(х) ® (h(х), g(х)) = 1 = > uh + vg = 1. Т.к. g(a ) = 0, u (a ) h (a ) = 1 u(a ) = . Следовательно, = f (a )u(a ) , где f(х), u(х) О Р[ х] , а f (a ), u(a )О Р[ a ] . Таким образом удалось освободиться от иррациональности в знаменателе дроби, а сделать это можно так:

рассмотрим h(х) и g(х) – минимальные a , если a

с помощью алгоритма Евклида подобрать u(х) такой, что h(х) g(х) + v(х) g(х) = 1;

найти u(a );

= f (a )u(a )

Вопрос 10. Кольцо многочленов от одной переменной.

Вопрос предполагает решение проблемы построения кольца многочленов как алгебры и решение проблемы о корнях многочлена.

Для построения кольца многочленов как алгебры напомним определение алгебры.

Определение 1. Алгеброй называется упорядоченное множество двух множеств , где множество элементов любой природы, а V – множество операций.

Одной из алгебр является кольцо.

Определение 2. Кольцом называется алгебра с двумя бинарными операциями – сложение и умножение -, удовлетворяющих следующим свойствам:

< K, +> - аддитивная абелева группа;

“ ґ ”- ассоциативная операция;

Сложение и умножение связаны дистрибутивным законом.

Для построения кольца многочленов зададим кольцо К и введем понятие многочлена.

Определение 3. Многочленом f(x) называется сумма a _n x ⁿ +a _n-1 x ^n-1 +...+a ₁ x+a ₀ , где a _iО K, x – неизвестное, xП K, x ⁰ =1, 1·x= x . a _i называют коэффициентами многочлена, a _n - старшим, a ₀ – свободным членом.

Определение 4. Суммой двух многочленов и называется многочлен h(x)=f(x)+g(x) , h(x)=c _k x ^k +...+c ₀ _, где c _i =a _i +b _i . Определение 5. Произведением двух многочленов и называется многочлен 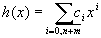, где .

Обозначим множество всех многочленов с коэффициентами из кольца K через K[x] и рассмотрим алгебру <K[x], +, ґ > . Докажем теорему о том, что эта алгебра является кольцом.

Теорема 6. Алгебра многочленов <K[x], +, ґ > , с коэффициентами из кольца K образует кольцо.

g 1. f(x)+(g(x)+h(x))=(f(x)+g(x))+h(x)

f(x)+g(x)=g(x)+f(x)

f(x)(g(x)h(x))=(f(x)g(x))h(x)

f(x)(g(x)+h(x))=f(x)g(x)+f(x)h(x)

Ассоциативность сложения и умножения, коммутативность сложения и дистрибутивные законы непосредственно вытекают из введенных нами операций над многочленами.

2. - называют нулевым многочленом, легко проверить, что , т.е. - выполняет роль нулевого элемента в алгебре K[x] .

f(x)=(-a _n )x ⁿ +...+(-a ₁ )x+(-a ₀ )=-f(x) – называют противоположным многочленом для многочлена f(x) , он выполняет роль противоположного элемента в алгебре. Так как все аксиомы кольца выполняются, то <K[x],+,ґ > - кольцо, которое обозначают K[x] и называют кольцом многочленов над кольцом K .

Теорема 7. Если K область целостности, то K[x] тоже область целостности.

Для доказательства этой теоремы введем понятие степени многочлена.

Степенью многочлена f(x) называется максимальный показатель степени x с коэффициентом отличным от нуля. Обозначение: deg f(x)=n, где a _n№ 0 .

Степень многочлена обладает свойствами:

deg (f + g) Ј max (deg f, deg g); deg (fg) = deg f + deg g , если K – область целостности. Доказательство свойств степени многочлена осуществляется на основе двух аргументов: во-первых, на основании выполнения операций; во-вторых, на основании целостности K.

Приступим к доказательству теоремы. Требуется проверить выполнимость: (1) коммутативности умножения и (2) отсутствие делителей нуля.

коммутативность умножения следует из определения умножения многочленов над областью целостности, где умножение элементов коммутативно.

f(x)№ , deg f(x)=nі 0, g(x)№

, deg g(x)=mі 0,

deg (f(x)g(x))=deg f(x)+deg g(x)= n+m і 0 Ю deg (fg) = n+m і 0 Ю $ c _{n+m №} 0 Ю (fg)№ , это и доказывает отсутствие делителей нуля в K[x] , где K – область целостности.

Пусть возникла ситуация, где требуется многочлен f(x) = a _n x ⁿ +...+a ₁ x+a ₀ разделить на двучлен (x-a) . Это можно сделать с помощью алгоритма, который принято в математике называть схемой Горнера. Построим этот алгоритм.

f(x) = (x-a)g(x)+r(x), где f(x) = a _n x ⁿ +...+a ₁ x+a ₀ , g(x)= b _n x ⁿ +...+b ₁ x+b ₀ .

Воспользуемся свойством степени, получим:

deg f(x) Ј deg [(x-a)g(x)+r(x)]Ј max[deg (x-a)g(x), deg r(x)]

deg (x-a)g(x)=deg (x-a)+deg g(x) . Из этих равенств можно сделать вывод, что m=n-1 , deg r(x)=0 , т.е. r(x) – число, т.е. a _n x ⁿ +a _n-1 x ^n-1 +...+a ₁ x+a ₀ =(x- -a)b _n x ⁿ +...+b ₁ x+b ₀ +r . Раскроем скобки справа и приравняем коэффициенты многочленов. Для удобства одновременно воспользуемся схемой.

	a _n	a _n-1	...	A ₂	a ₁	a ₀
a	b _n-1	b _n-2 =ab _n-1 +a _n-1	...	b ₀ =ab ₁ +a ₁	b ₀ =ab ₁ +a ₁	r=ab ₀ +a ₀

a _n x ⁿ =b _n-1 x ⁿ Ю b _n-1 =a _n

a _n-1 x ^n-1 =b _n-1 x ⁿ (-a)+b _n-2 x ^{n-1 Ю} a _n-1 =b _n-1 (-a)+b _{n-2 Ю} b _n-2 =a _n-1 +ab _n-1

b ₁ =ab ₂ +a ₂ , b ₀ =ab ₁ +a, r=ab ₀ +a ₀ .

Введем понятие корня многочлена.

Определение 8. Число x=a называется корнем многочлена f(x) , если значение многочлена f(a) равно нулю.

Рассмотрим теорему Безу о делении многочлена на двучлен (x-a).

Теорема 9. (Безу) Остаток от деления многочлена f(x) на двучлен (x-a) равен f(a).

g f(x), (x-a ). Поделим, f(x)=(x-a)g(x)+r , мы установили, что r – число. Подставим x=a в равенство, получим f(a)=0g(a)+r , откуда вытекает утверждение теоремы f(a) = r .

Из теоремы вытекает следствие: f(x)M (x-a) Ы x=a корень уравнения.

Ю f(x) M (x-a) Ю f(x)=(x-a)g(x)+f(a) (по теореме Безу), f(a)=0 Ю x=a корень f(x)

Ь Пусть x=a корень многочлена, т.е. f(a)=0 Ю f(x)=(x-a)g(x) (по теореме Безу), т.е. f(x) M (x-a).

Вопрос 11. Кольцо многочленов над полем комплексных чисел.

В алгебре многочленов имеют место две взаимно пересекающиеся, взаимно дополняющие линии. Это вопросы существования и количества корней многочлена и разложение многочлена на неприводимые множители.

В вопросе представлено решение этих аспектов для кольца многочленов над полем комплексных чисел, т.е. для кольца C[x] , где C – поле комплексных чисел.

Итак, пусть P – поле.

Определение 1 . Поле P называется алгебраически замкнутым, если любой многочлен положительной степени имеет в этом поле корень. Алгебраической замкнутостью обладает поле C , это решается основной теоремой алгебры.

Теорема 2. Любой многочлен положительной степени из кольца C[x] обладает по крайней мере одним корнем. Примем эту теорему без доказательства в силу того, что она требует предварительного доказательства ряда теорем из математического анализа.

Из основной теоремы алгебры вытекает ряд следствий, их и рассмотрим.

Следствие 3. Неприводимым над полем C многочленом является многочлен только первой степени.

Для доказательства этого утверждения введем определения приводимого и неприводимого многочлена. Многочлен f(x)О P[x] называется приводимым, если его можно представить в виде произведения двух многочленов меньшей положительной степени. В противном случае многочлен называется неприводимым.

Приступим к доказательству следствия 3.

Пусть дан f(x)О C[x]. Пусть он приводим. Покажем, что

рассмотрим f(x)=a ₁ x+a ₀ , degf(x)=1 . Предположим, что f(x) – приводим. Тогда по определению приводимого многочлена f(x)=f ₁ (x)f ₂ (x) , где degf ₁ (x)>0 , degf ₂ (x)>0. Однако по условию degf(x)=1=1+0=0+1 , то есть degf ₁ (x)=0И degf ₂ (x)=0 , что противоречит свойству степеней. Полученное противоречие и доказывает неприводимость многочлена ( а ₁ х+а ₀ ).

Пусть deg f(x)>1 , тогда по основной теореме алгебры он обладает корнем. Пусть таким корнем будет х=а . По следствию из теоремы Безу: f(x)=(x-a)f ₁ (x) . Так как deg(x-a)=1, degf(x)>1, deg(x-a)f ₁ (x)=deg(x-a)+degf ₁ (x) , то degf(x)>0 ; то есть f(x) – приводим, что противоречит условию. Таким образом, неприводимым над полем С является только многочлен первой степени.

Следствие 4 . Если f(x)О C[x], degf(x)=nі 1 , то его можно представить в виде:

с(x-a ₁ )(x-a ₂ )...(x-a _n ), (*)

где a _i – корни его, а сО С.

g Пусть f(x)=c ₁ x+c ₀ =c ₁ =c ₁ (x-a ₁ ), где , то есть для многочлена f(x) утверждение верно: он представляется в виде (*) и а ₁ – корень его, а с ₁ – старший коэффициент.

Далее, проведем доказательство методом математической индукции. Пусть теорема верна для многочлена степени меньшей или равной ( n-1 ), то есть

f(x)=c(x-a ₁ )...(x-a _n-1 ) , где a ₁ , a ₂ , ..., a _n-1 – его корни, а с – старший коэффициент.

Пусть f(x) – неприводим, а это возможно только для n=1 , для этого случая теорема верна. Либо f(x) – приводим, тогда f(x)=g(x)h(x) , где степени g(x) и h(x) меньше n , для них теорема верна. В силу свойства степени f(x)=c(x-a ₁ )...(x-a _n ), то есть множителей будет ровно n . По следствию из теоремы Безу а _i – корни f(x) , если расткрыть скобки в правой части и воспользоваться равенством многочленов, то с – старший коэффициент f(x) . Теорема доказана.

Из этого в следствии с необходимостью вытекает еще два.

Следствие 5. Количество комплексных коней многочлена f(x)О C[x] совпадает с его степенью.

Следствие 6. Любой многочлен f(x)О C[x] положительной степени n можно представить в виде:

f(x)=c(x-a ₁ )a ₁ (x-a ₂ )a ₂ ...(x-a _k )a _k , где a ₁ +...+a _k =n, a _i – его корни. Такое представление носит название канонического. Возможность такого представления вытекает из следствия (4) и допустимости повторяющихся корней, то есть кратных корней многочлена.

В теории многочленов над С имеет место теорема, устанавливающая связь между корнями многочлена и его коэффициентами.

Теорема 7 . Пусть f(x)О C[x], degf(x)=n, a _n =1 (то есть f(x) – нормирован), тогда как известно, f(x)=(x-a ₁ )(x-a ₂ )...(x-a _n ), где имеет место соотношение:

а ₀ = (-1) ⁿ a ₁ a ₂ ... a _n ;

a ¹ = (-1) ^n-1 (a ₁ a ₂ ... a _n-1 + ... + a ₂ a ₃ ... a _n );

. . . . . . . . .

a ^n-2 = a ₁ a ₂ + a ₁ a ₃ + ... + a _n-1 a _n ;

a ^n-1 = -(a ₁ + a ₂ + ... +a _n );

эти соотношения называются формулами Виета. Однако, справедливости ради, надо отметить, что Виет нашел эту зависимость только для случая положительных корней, в общем виде эта теорема установлена А. Жирарое.

Вопрос 12 Кольцо многочленов над полем действительных чисел (R).

В алгебре имеет место теория многочленов. Многочлен введен по определению как выражение f(x)=a _n x ⁿ +a _n-1 x ^n-1 +...+a ₁ x+a ₀ , где a _iО K – кольцо , x ⁰ =1, 1·x= x . Введение операций “+” и “ґ ” многочленов позволило построить алгебру многочленов, которой является кольцо многочленов над кольцом К и обозначается К[x] . Особый интерес представляет теория многочленов, когда вместо кольца К взято поле. Такими числовыми полями являются C, R, Q .

В силу существования операции деления в поле, стало возможным рассматривать два взаимосвязанных вопроса в теории многочленов: корни многочлена и разложение многочлена на неприводимые многочлены.

Рассмотрим решение этой проблемы для кольца многочленов над R.

Теорема 1. Комплексные корни f(x)О К[x] , то есть с действительными коэффициентами попарно сопряженными.

n Пусть f(x)О К[x] , и пусть z=a+bi; a,bО R комплексное число, являющееся корнем f(x) , причем degf(x)і 2 в противном случае f(x) комплексных корней иметь не может. Покажем, что = a–bi , b№ 0 тоже является корнем f(x).

f( )=a _n ⁿ +a _n-1 ^n-1 +...+a ₁ +a ₀ = (воспользуемся свойством сопряжения) = = , то есть является корнем f(x) , что и требовалось доказать.

Рассмотренная выше теорема позволяет доказать теорему о неприводимом многочлене из R[x] . Напомним определение приводимого и неприводимого многочленов.

f(x) называется неприводимым, если его можно представить в виде произведения двух многочленов меньшей положительной степени и неприводимым, если этого сделать нельзя.

Рассмотрим f(x)= a ₁ x+a ₀ , a _iО R . его нельзя представить в виде произведения двух многочленов меньшей положительной степени в силу того, что 1=1+0=0+1 .

Решать будем вопрос о приводимости и неприводимости многочлена f(x)О R[x] степени большей или равной 2.

Теорема 2. Неприводимый многочлен f(x)О R[x], degf(x)=nі 2 ассоциирован с многочленами (x-a) ² +b ² ,где x=a+bi комплексный его корень.

n Пусть f(x)О R[x], degf(x)=nі 2 , пусть x=a+bi, b№ 0 – корень f(x) , он неприводим.

Прежде всего отметим, что у такого многочлена нет действительных корней, иначе бы f(x)=(x-a) f ₁ (x) (следствие из теоремы Безу), что противоречило бы его неприводимости.

По теореме о сопряженности мнимых корней многочлена с действительными коэффициентами f(x) обладает еще одним корнем x ₂ =a–bi , где x ₂ = .

Рассмотрим (x-x ₁ )(x-x ₂ )=(x-a) ² +b ² . (*)

Разделим f(x) на многочлен (*), получим:

f(x)=[(x-a) ² +b ² ]g(x)+r(x).

Так как степень делителя равна 2, то degr(x)<2 , то есть r(x)=cx+d . Подставим в (1) x1=a=bi и x ₂ =a-bi, мы получим:

Так как b№ 0 , то c=0 , тогда d=0 , то есть r(x)=.

Это означает, что f(x)M (*). Но f(x) – неприводим, потом deg g(x)=0 , то есть g(x)О R . Что и подтверждает ассоциированность f(x) и (*).

Теорема 3. Рассмотренная выше теорема позволит сделать ряд выводов:

Неприводимыми многочленами над R могут быть многочлены не выше второй степени.

Многочлен f(x)О R[x], degf(x)і 1 может быть представлен в виде:

, где если среди корней есть кратные, то можно представить и в виде (*):

, где S _i – кратности корней, а t _j – кратности сопряженных мнимых его корней. Представление (*) называется каноническим представлением f(x).

Теорема 4. Теоремы (1), (3) позволяют сделать с очевидностью вывод о том, что четность действительных корней совпадает с четностью его степени.

Вопрос 13. Кольцо многочленов над полем рациональных чисел (Q).

Теория многочленов утверждает, что множество многочленов f(x) = a _n x ⁿ + …+ a ₁ x + a ₀ ,

где a _i ∈ K – кольцо, x ⁰ =1, x∈K, 1∙x=x с операциями сложения и умножения образуют кольцо многочленов над кольцом K и обозначают K [ x ].

Особый интерес представляет теория многочленов, когда вместо кольца K рассматривается поле P . В силу того, что в поле P есть операция деления, становится возможным построить теорию корня многочленов и теорию приводимых и неприводимых многочленов. Рассмотрим, как решается эта проблема в Q [ x ].

Напомним, что корнем f(x) называется такое число x = a , что f(a) = 0 .

f(x) называется неприводимым, если его нельзя представить в виде двух многочленов меньшей положительной степени, в противном случае его называют приводимым.

Итак, пусть Q [ x ], f(x)∈ Q [ x ], где f(x) = a _n x ⁿ + …+ a ₁ x + a ₀ …(1), сформулируем и докажем теорему о рациональных корнях многочлена с целыми коэффициентами. Если многочлен имеет рациональные коэффициенты, то он легко преобразуется к ему ассоциированному с целыми коэффициентами. Поэтому теорию существования и нахождения корней f(x)∈ Q [ x ] рассматривают именно для такого варианта, т.е. f(x)∈ Q [ x ], а a _i ∈ Z.

Теорема 1: Если 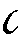∈Q , где (p,q)=1, является корнем многочлена (1)… f(x) = a _n x ⁿ + …+ + a ₁ x + a ₀ , a _i ∈ Z , то p является делителем свободного члена, а q -делителем старшего коэффициента a _n .

Если Q корень f(x) , то f 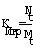=0. Подставим в (1) вместо x , получим

0= a _n + …+ a ₁ + a ₀ , приведём к общему знаменателю, получим

0= a _n p ⁿ + a _n-1 p ^n-1 q+…+ a ₁ p q ^n-1 + a ₀ q ⁿ …(2).

Преобразуем (2) :

2.1 : 0 = a _n p ⁿ + q(a _n-1 p ^n-1 +…+ a ₁ p q ^n-2 + a ₀ q ^n-1 ) ⇒ a _n p ⁿ + q Q ∶ q, qQ ∶ q

⇒ a _n p ⁿ ∶ q, (p,q)′→ a _n ∶ q , т.е. q- делитель старшего коэффициента;

2.2 : 0 = p(a _n p ^n-1 +…+ a ₁ q ^n-1 ) + a ₀ q ⁿ ) ⇒ pQ + a ₀ q ⁿ ∶ p, pQ ∶ p, ⇒ a ₀ q ⁿ ∶ p, (q,p)=1 ⇒ a ₀ ∶ p, т.е. p -делитель свободного члена, что и доказывает теорему.

Следствие 2: Если f(x)∈ Q [ x ], а a _i ∈Z , a _n = 1 , то он обладает только целыми корнями, которые находятся среди делителей свободного члена.

Истинность этого утверждения очевидна в силу того, что a _n = 1, а делители 1 являются только ±1, следовательно, q= ±1 и ∈Z . Т.к. = ± p∈Z находятся среди делителей, то утверждение верно.

Решим проблему неприводимости многочлена из Q [ x ], вернее о степени такого многочлена.

Решение этой проблемы предложено Эйзенштейном и носит название критерий Эйзенштейна о неприводимости многочлена в Q [ x ]. Заметим, что решение этой проблемы тоже есть смысл рассматривать для f(x)∈ Z [ x ], поскольку Q является полем частных области целостности Z .

Теорема 3: Пусть f(x)= c _n x ⁿ + …+ c ₁ x + c ₀ , c _i ∈Z . Пусть все коэффициенты f(x) , кроме старшего, делятся на p ² . Тогда f(x) неприводим в Z [ x ].

Доказательство проведём методом от противного.

Пусть f(x)∈ Q [ x ] или f(x)∈ Z [ x ] приводим, т.е. существуют такие g(x), h(x)∈ Z [ x ], что

f(x) = (a ₀ +…+a _k x ^k )(b ₀ +…+ b _m x ^m ) = g(x)·h(x), (a _k ≠ 0, b _m ≠ 0, k + m = n, причем 1≤ k, m < n).

Тогда c ₀ = a ₀ ·b ₀ , c _n = a _k ·b _m . Так как c ₀ ∶ p, c ₀ не∶ p ₂ , c ₀ = a ₀ ·b ₀ ⇒ a ₀ не∶ p Λ b ₀ не∶ p ; пусть a ₀ ∶ p,

b ₀ не∶ p . Так как c _n не∶ p , то a _k не∶ p, b _m не∶ p, тогда у g(x) есть коэффициент делящийся на p и неделящийся на p . Пусть a _s коэффициент g(x) с наименьшим s таким, что a _s не∶ p, т.е. a ₀ , a ₁ , …, a _s-1 ∶ p, а a _s не∶ p .

Найдем c _s = a _s b _s + (a _s-1 b ₁ + a ₀ b _s ) (s<n), т.к. a _s не∶ p, b ₀ не∶ p, то a _s b ₀ не∶ p, число (a _s-1 b ₁ + a ₀ b _s ) ∶ p, по свойству делимости в кольце Z, c _s не∶ p, s<n, а это противоречит условию. Получено противоречие в силу предположения, что f(x) - приводим. Что и доказывает теорему о неприводимости f(x) .

Следствие 4 : Если p – простое число и n – любое целое положительное число, то многочлен x ⁿ -p неприводим в Q [ x ].

Теорема 3 и следствие 4 позволяют сделать вывод о том, что в Q [ x ] существуют неприводимые многочлены любой степени. Поэтому решение проблемы нахождения корней f(x) и разложения его на неприводимые многочлены затрудненно и требует в каждом конкретном случае особого подхода.

Вопрос 14. Простое алгебраическое расширение поля.

Пусть дано поле P . P[x] - кольцо многочленов от одной переменной над полем P . Обратимся к понятию алгебраической замкнутости поля P . Напомним, что поле Р называется алгебраически замкнутым, если любой многочлен f(x)О P[x] обладает хлтя бы одним корнем. Введем такое понятие: элемент a О Р называется алгебраическим над полем Р , если существует f(x)О P[x] , для которого a является корнем.

Пусть дано поле Р и a П Р , a О F – поле.

Определение 1. Простым расширением поля Р с помощью элемента a называется наименьшее подмножество поля F , содержащее Р и a . Простое расширение поля Р с помощью a О F обозначается Р(a ) .

В вопросе решается проблема о строении Р(a ) и возможности применения этой теории для освобождения знаменателя дроби от алгебраической иррациональности. Для решения обозначенной проблемы рассмотрим Р[a ]={f(a )/f(x)О P[x]} , где Р[a ]={a ₀ +a _1a +...+a _na ⁿ /a _iО P, nО N} .

Легко проверить, что Р[a ] подкольцо поля Р(a ) .

Теорема 2. Пусть Р[x] – кольцо над Р , Р(a ) – простое расширение Р с помощью элемента a . Пусть y : Р[х] на Р[a ] – отображение такое, что y (f(x))=f(a ) . Тогда:

1 ⁰ . " aО P, y (a)=a ;

2 ⁰ . y (x)=a ;

3 ⁰ . y – гомоморфизм и эпиморфизм;

4 ⁰ . Ker y ={f(x)О Р[x]/ f(a )=0О Р[a ]};

5 ⁰ . Фактор-кольцо Р[х]/Ker y изоморфно кольцу Р[a ].

n 1 ⁰ и 2 ⁰ следуют из определения y .

3 ⁰ : y (f(x)+g(x))= f(a )+g(a ), y (fg)=f(a )g(a ), y (1)=1, это проверяется непосредственно, поэтому y – гомоморфизм; " f(a )О Р[a ], $ f(x)О Р[x], y (f(x))=f(a ) Ю y – эпиморфизм.

4 ⁰ : следует из существования Ker f для гомоморфизма и из определения y .

Рассмотрим 5 ⁰ . Так как Ker y – идеал Р[х] , то становится возможным Р[х] факторизовать, получить Р[х]/Ker y , тогда по основной теореме об эпиморфизме колец Р[х]/Ker y є Р[a ].

e : Р[x]® Р[x]/Kery , e (f(x))=Kf(x).

j : Р[x]/Kery ® Р[a ], где

j (Kf(x))=f(a )Ю j – изоморфизм.

Следствие 3. Если a - трансцендентный элемент над полем Р , то Р[х]@ Р[a ] .

n В силу трансцендентности a над Р , Kery ={0} и Р[x]/{0}@ Р[a ], кроме того e – изоморфизм, то есть Р[x]/{0}@ Р[x] следовательно, Р[x]@ Р[a ].

Определение 4. Пусть Р[х] – кольцо многочленов над полем Р . Пусть a – алгебраический элемент над полем Р . Минимальным многочленом * a над Р называется нормированный многочлен наименьшей степени, для которого a является корнем.

Обозначим минимальный многочлен для a над Р через g(x) , deg g(x)=n называют степенью алгебраического элемента a над Р.

Легко показать:

g(x) существует для каждого алгебраического элемента;

g(х) – неприводимый многочлен в Р[х] над Р ;

g(x) для a определяется однозначно.

– вытекает из определения алгебраического элемента.
– из определения минимальности g(x) .
– из предположения, что существует два многочлена * g и h и их неприводимости, они ассоциированы, а так как они неприводимы, то g(x)=h(x) .

Теорема 5. Пусть a алгебраический элемент степени n над Р (a П Р ) и g(x) – его минимальный многочлен степени n , тогда имеют место:

1 ⁰ . Если f(a )=0 , где f(x)О Р[х], то f(x)M g(x) ;

2 ⁰ . Р[х]/(g(f))@ Р[х] ;

3 ⁰ . Р[х]/(g(f)) – поле;

4 ⁰ . Р[a ]=Р(a ).

n Пусть a корень f(x) , то есть f(a )=0 , известно, что g(a )=0 , тогда (f,g) либо 1, либо нет. Первое невозможно, так как по известной теореме f(x)M (x-a ) и

g(x)M (x-a ) . Следовательно, (f,g)№ 1 , то есть они не являются взаимно простыми, поэтому f(x) делится на g(x) .

Зададим гомоморфизм y : Р[х]® Р[a ], y (f(x))=f(a )Ю Ker y ={f(x),f(a )=0} состоит из многочленов, делящихся на g(x), поэтому Ker y =J=(g(x)) – идеал Р[х]Ю Р[х]/(g(x)) @ Р[a ] (*), так как Р[a ]М Р(a ) , то Р[a ] – область целостностиЮ Р[х]/(g(x)) в силу (*) тоже область целостности. Покажем, что любой элемент из Р[х]/(g(x)) ненулевой обратимый.

Пусть смежный класс, , то f(a )=0 , тогда f(x) не делится на g(x)Ю ( f(x),g(x))=1Ю , но Ю Ю , что и требовалось доказать, то есть Р[х]/(g(x)) – поле, а так как эта алгебра изоморфна Р[a ] , то Р[a ] тоже поле являющееся подполем поля Р(a ) . Но Р(a ) минимальное подполе поля F , следовательно, Р(a ) М Р[a ] , откуда получаем, что Р[a ]=Р(a ) .

Эта теорема позволяет установить строение простого алгебраического расширения Р(a ).

Пусть a - алгебраический элемент над P , а Р(a ) – простое алгебраическое расширение P , пусть степень a равна n>0 . Тогда

Теорема 6. Любой элемент поля Р(a ) однозначно представим в виде линейной комбинации n элементов 1,a ,...,a ^n-1 с коэффициентами из P .

Вопрос 15. Простые и составные числа .

Рассмотрим N – натуральные числа. Введем понятие простого и составного числа.

Опр.1 N ' а называется делящимся на число вО N , в > 0, если существует такое число с, что а = вс, при этом а – делимое, в – делитель, с – частное.

Все натуральные числа, в связи с отношениеми делимости на , разбиваются на группы: { 0} , { 1} , { р ₁ , р ₂ ,…,…} , { а ₁ , а ₂ ,…} , где 1 обладает только один делитель, р _i – двумя, а для а _i существует более двух.

Опр.2 Натуральное число р называется простым, если оно имеет ровно два различных делителей. (1 и само число р), составным, если имеет более двух делителей.

Введенное определение позволит выражать числа натуральные через простые. Это описывается теоремой, которую называют основной теоремой арифметики.

Теорема. 3 Любое n О N , n > 1 можно единственным образом представить в виде произведения простых чисел с точностью до перестановки сомножителя.

В теореме содержится две теоремы: о существовании разложения и его единственности.

(7) Пусть n О N , n > 1. Для доказательства исследуем метод математической индукции.

n = 2, 2 – простое число, следовательно n = 2 и есть его разложение.

Предположим, что для любого натурального числа, меньшего n, теорема верна и докажем для n.

Пусть дано натурально n, если оно простое, то это и есть его разложение. Если n составное, тогда n = вс, где в,с О N и меньше n. По предположению индукции разложение их на простые множители существует, поэтому оно существует и для n. На основании принципа математической индукции, можно утверждать истенность теоремы для любого n О N , n > 1.

(!) Докажем единственность разложения на простые множетели методом математической индукции.

n = 2, 2 = 2. Разложение единственное.

Допустим, что для любого числа натурального, меньшего n утверждение справедливо и докажем для n. Если n простое число, то это и есть его разложение и оно единственно. Если n составное, то оно допустит разложение на простые числа. Предположим, что таких разложений оказалось два: n = p ₁ p _{2 ј} p _к = q ₁ q ₂ ^… q _s (1). Из равенства (1) видно, что “правая часть” делится на p ₁ . А т.к. в “правой части числа простые”, то

существует число q _i , которое делится на p ₁ ;

(p ₁ , q _i ) = 1. Следовательно, p ₁ = q _i . Пусть q _i = q ₁ , разделим обе части равенства (1) на p ₁ , получим, что и “левая часть” и “правая часть” числа натуральные, меньше n, а для них разложение единственное с точночтью до перестановки сомножителя. Поэтому при соответственно мы получаем, что n = p ₁ p _{2
ј} p _к – разложение n и это разбиение единственное. Что и требовалось доказать.

Если среди простых множителей окажутся равные, то их объединяют в степень и получают представление n О N в виде: , которое называют каноническим разложением натурального числа.

В теории натуральных чисел имеет место теорема, решающая вопрос о количестве простых чисел во множестве N .

Теорема 4. (Евклида) Множество простых чисел в N бесконечно.

Проведем доказательство методо от противного.

Пусть простых чисел конечное число: p ₁ p _{2 ј} p _к . Рассмотрим N = p ₁ p _{2 ј} p _к+1 . Исследуем полученное число:

1) N > 1 = > оно простое или составное; N № p _i , i = 1, к ;

2) N p _i , , i = 1, к = > , т.к. при делении на p _i получен остаток 1;

N – составное. Если N составное, то ему надлежит делиться на 1, N и еще на какое-нибуть простое число (см. ниже), но это не так, поэтому N не является составным. Полученное противоречие и доказывает теорему.

Теорема 5. Наименьший, отличный от 1 делитель составного числа, является простым числом.

Пусть n О N имеет делители, отличные от 1. Обозначим тот делитель, который будет наименьшим среди всех делителей. Пусть это натуральное число к, т.е. n = к ^. m; к, m О N , к > 1. Исследуем к.

Если к = p – простое число, то теорема верна.

Если к – составное число, то к = к ₁ m ₁ , тогда n = к ₁ (m ₁ m), n к ₁ , к ₁ < к, что противоречит выбранному наименьшему значению. Это и доказывает теорему.

Достаточно часто в математике приходитс для числа а О N выяснять, является оно простым или составным. Для решения подобных задач предложен способ, носящий название “решето Эратосфена…” или способа отсеивания чисел кратных 2,3,…,p,… .

Опишем этот способ.

Если даны числа натурального ряда: 1,2,3,4,5,…,n, то для установления какими они являются: простыми или составными, поступают так: вычеркивают 1,2 и каждое второе, ибо каждое второе начинается от 3, делится на 2, поэтому является составным. Затем повторяем эту процедуру для 3. 3 вычеркивается и каждое третье, ибо 6 – третье по счету за 3, делится на 3. названную процедуру повторяют до простого числа с не превосходящего . Оставшиеся числа являются простыми.

Такой алгоритм можно использовать и для установления чисел в промежутке от n ₁ до n ₂ .

Опишем его спецификацию . Если надо установить какие числа в промежутке от n ₁ до n ₂ являются простыми, то поступим так:

выясним простое или составное является число n ₁ :

Проверим его делимость на 2,3,5,…p ≤ . Если оно не делится на эти простые числа, то оно простое;
Если оно делится хотя бы на одно из этих чисел, то оно составное.

при выяснении простого числа n, одновременно поступаем так:

2.1 если n ₁ 2, то вычеркивают его и каждый второй (как в первом случае); и переходим к (n ₁ + 1);

2.2 если n ₁ 2, то к числу добавляем 1 и вычеркиваем n ₁ + 1 и любое второе за ним;

2.3 если было 2.1, то переходим к (n ₁ + 1) и проверяется делим его на 3, повторяем процедуру решета Эратосфена переходит к (n ₁ + 2);

2.4 Если было 2.2, то проверяют делимость на 3;

2.4.1. если n ₁ 3, то проверяю решето Эратосфена и переходят следующему.

не вычеркнутому числу и исследуют его делимое на 5;

2.4.2. если n ₁ = 3q + r, то в зависимости от r = 1 или r = 2, добавляем 1 или 2 и

n ₁ + 1, n ₁ + 2.

И любое третье по счету и т.д.

2.5 Если n ₁ оказалось простым, то все не вычеркнутые числа тоже простые. Если n ₁ оказалось составным, а n _i – простое, то все стоящие за n _i числа остальные простые.