

Определение. Функция называется элементарной по Кальмару, если ее можно получить й из функций s 1 , I n m , x+y, x-y, S, а также конечного применения операций суммирования и мультиплицирования.
Определим пять классов функций, элементарных по Кальмару.
L 1 Класс функций, получаемый из функций s 1 , I n m , x+y, x-y, S, а также конечного применения операций суммирования и мультиплицирования.
L 2 Класс функций, получаемый из функций s 1 , I n m , x-y, 2 x ,S, а также конечного применения операции суммирования.
L 3 Класс функций, получаемый из функций s 1 , I n m , x-y, x*y, 2 x ,S, а также конечного применения операции ограниченной минимизации.
L 4 Класс функций, получаемый из функций s 1 , I n m , x-y, x+y 2 x ,S, а также конечного применения операции ограниченной рекурсии.
L 5 Класс функций, получаемый из функций s 1 , I n m , x-y, x*y, S, а также конечного применения операции мультиплицирования.
Доказательство будем проводить по следующей схеме:
1. L 1 L 2 L 3 L 4 L 1
2. L 1 L 5
3. L 5 L 3
Докажем, что L 1 L 2 (для этого выразим 2 x через функции L 1 )
![]()
Докажем, что L 2 L 3 (для этого выразим x*y и операцию ограниченной минимизации через функции L 2 )
![]()
Пусть
![]() тогда
тогда
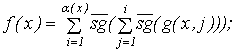
![]()
Докажем, что L 3 L 4 (для этого выразим x+y и операцию ограниченной рекурсии через функции L 3 )
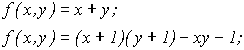
Выразим операцию ограниченной рекурсии на основании следующего свойства функции Геделя.
![]()
Пусть
![]() тогда
тогда
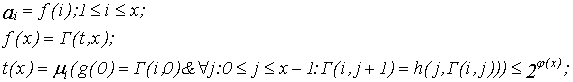
Отношение, примененное в операция конечной минимизации, является элементарным по Кальмару.
Докажем, что L 4 L 1 (для этого выразим операции суммирования и мультиплицирования через функции L 4 )
Выразим м3ультиплицирование через ограниченную рекурсию.
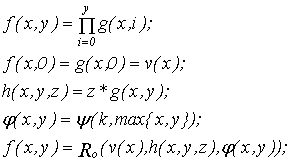
Где (x,y)-к-ступенчатая функция.
Выразим суммирование через ограниченную рекурсию.
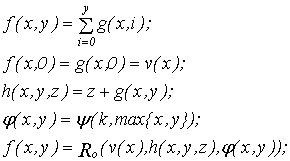
Докажем, что L 1 L 5 (для этого выразим x*y через функции L 5 )
![]()
Докажем, что L 5 L 3 (для этого выразим 2 x и операцию ограниченной минимизации выразим через функции L 5 )
![]()
Пусть
![]() тогда
тогда
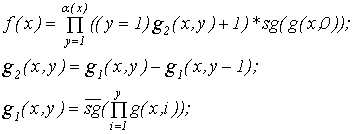
Эквивалентность классов доказана.