Определение: Элемент наилучшего приближения – L – линейное многообразие, плотное в E. " e " x Î E $ u: ║x-u║< e

Теорема: Для любого элемента нормированного пространства существует хотя бы один элемент наилучшего приближения из конечномерного подпространства.

Теорема: Для элемента из строго нормированного конечномерного пространства существует единственный элемент наилучшего приближения из конечномерного подпространства.

Теорема: Рисса о существовании почти ортогонального элемента. E-НП L Ì E, " e Î (0,1) $ z e Î E\L ║z e ║=1 r (z e ,L)>1- e

Определение: Полное нормированное пространство- любая фундаментальная последовательность сходиться.

Теорема: О пополнении нормированного пространства. Любое нормированное пространство можно считать линейным многообразием, плотным в некотором полном нормированном пространстве.

Определение: Гильбертово пространство – нормированное пространство, полное в норме, порожденной скалярным произведением.

Теорема: Для любого элемента гильбертова пространства существует единственный элемент наилучшего приближения в конечномерном подпространстве гильбертова пространства.

Определение: L плотное в E, если " x Î E $ u Î L: ║x-u║< e

Теорема: Чтобы L было плотно в H ó ортогональное дополнение к L состояло только из нулевого элемента.

Определение: Сепарабельное – нормированное пространство, содержащее некоторое счетное плотное в нем множество.

Определение: Ортогональное дополнение – множество элементов ортогональных к элементам данного пространства.

Определение: Линейный оператор – отображение, для которого A(ax+by)=aAx+bAy

Определение: Непрерывный оператор – Ax à Ax 0 при x à x 0

Определение: L (X,Y) – пространство линейных операторов

Теорема: Пусть X и Y – полные НП и A – непрерывен на некотором подпространстве пространства X, тогда он непрерывен на всем X.

Определение: Ограниченный оператор - " ¦x║≤1 $ с: ║Ax║≤c

Теорема: A – ограниченный ó " x Î X ║Ax║≤c║x║

Теорема: Для того чтобы А был непрерывен ó чтобы он была ограничен

Теорема: {A n } равномерно ограничена è {A n }- ограничена.

Теорема: {A n x} – ограниченно ó {║A n ║}- ограничена.

Определение: Сильная (равномерная) сходимость ║A n -A║ à 0, n à ¥ , обозначают A n à A

Определение: Слабая сходимость - " x Î X ║(A n -A)x║ Y à 0, n à ¥

Теорема: Для того, чтобы имела место сильная сходимость ó {A n } сходилась равномерно на замкнутом шаре радиуса 1

Теорема: Банаха-Штенгауза A n à A n à ¥ слабо è 1) {║A n ║}- ограничена 2) A n à A, x’ Ì X, x’=x

Теорема: Хана Банаха. A:D(A) à Y, D(A) Ì X è $ A’:X à Y 1) A’x=Ax, x Î D(A) 2) ║A’║=║A║

Определение: Равномерная ограниченность - $ a " x: ║x(t)║≤a

Определение: Равностепенная непрерывность " t 1 ,t 2 $ d : ║x(t 1 )-x(t 2 )║< e

Теорема: L (X,Y) полное, если Y – полное.

Определение: Ядро – {x Î X | Ax=0}

Определение: Сопряженное пространство – пространство функционалов X * := L (X,E)

Определение: Сопряженный оператор A * : Y * à X *

Теорема: Банаха A:X à Y и X,Y- полные нормированные пространства. Тогда $ A -1 и ограничен.

Определение: Оператор А – обратимый

Определение: Оператор А- непрерывнообратимый если 1) A- обратим, 2) R(A)=Y, 3) A -1 -ограничен.

Теорема: A -1 $ и ограничен ó $ m>0 " x Î X ║Ax║≥m║x║

Теорема: Рисса о представлении линейного функционала в гильбертовом пространстве. Пусть f:X à Y – линейный ограниченный функционал è $ ! y Î H " x Î H f(x)=(x,y)

Определение: M Ì X называется бикомпактным, если из любой ограниченной последовательности можно выделить сходящуюся к элементам этого же множества последовательность.

Определение: Множество называется компактным, если любая ограниченная последовательность элементов содержит фундаментальную подпоследовательность.

Теорема: Хаусдорфа. M Ì X компактно ó " e >0 $ конечная e -сеть

Теорема: Арцела. M Ì C[a,b] компактно ó все элементы множества равномерно ограничены и равностепенно непрерывны.

Определение: Компактный (вполне непрерывный) оператор – замкнутый шар пространства X переводит в замкнутый шар пространства Y.

Определение: s (X,Y) – подпространство компактных операторов

Теорема: Шаудера. A Î s (X,Y) ó A * Î s (X * ,Y * )

Линейные нормированные пространства

  1. Пространства векторов

    2. сферическая норма

    кубическая норма

    ромбическая норма

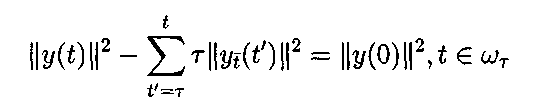    p>1

  2. Пространства последовательностей

    3. p>1

    или пространство ограниченных последовательностей

    пространство последовательностей, сходящихся к нулю

    пространство сходящихся последовательностей

  3. Пространства функций

пространство непрерывных на функций

пространство k раз непрерывно дифференцируемых на функций

£ p [a,b] пространство функций, интегрируемых в степени p (не Гильбертово)

- пополнение £ p [a,b] (Гильбертово)

Неравенство Гёльдера p,q>0

Неравенство Минковского