Понятие о центре тяжести было впервые изучено примерно 2200 лет назад греческим геометром Архимедом, величайшим математиком древности. С тех пор это понятие стало одним из важнейших в механике, а также позволило сравнительно просто решать некоторые геометрические задачи.

Именно приложение к геометрии мы и будем рассматривать. Для этого нужно ввести некоторые определения и понятия. Под материальной точкой понимают точку, снабжённую массой. Для наглядности можно себе физически представить материальную точку в виде маленького тяжёлого шарика, размерами которого можно пренебречь. В связи с этим будем часто указывать только числовое значение той или иной физической величины, но не будем отмечать её наименование, считая, что оно само собой подразумевается. Например, выражение: “В D ABC сторона BC равна a , а в вершине A мы помещаем массу a ” означает: “Длина стороны BC равна a ñàíòèìåòðàì, à ìàññà, ïîìåù¸ííà я в вершине A , равна a грамм”.

Если в точке A помещена масса m , то образующуюся материальную точку будем обозначать так: (A, m) . Иногда, когда это не может вызвать недоразумений, мы будем её обозначать одной буквой A . Массу m иногда называют “нагрузкой точки A ” .

Центром тяжести двух материальных точек (A, a) и (B, b) называется такая третья точка C , которая лежит на отрезке AB и удовлетворяет “правилу рычага” : произведение её расстояния CA от точки А на массу а равно произведению её расстоянию СВ от точки В на массу b ; таким образом,

.

Это равенство можно записать и так:

,

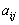то есть расстояние от центра тяжести двух материальных точек до этих точек обратно пропорциональны массам, помещённым в этих точках. Центр тяжести будет ближе к точке с большей массой. Из определения следует: если прямая проходит через центр тяжести двух материальных точек и через одну из них, то она пройдёт и через другую.

Центр тяжести двух материальных точек имеет весьма простой механический смысл. Представим себе жёсткий “невесомый” стержень АВ , в концах которого помещены массы а и b (рис. 1). “Невесомость” стержня практически означает, что его масса по сравнению с массами a и b настолько незначительна, что ею можно пренебречь. Центр тяжести С материальных точек (A, a) и (B, b) — это такая точка, в которой надо подпереть стержень AB , чтобы он был в равновесии.

Для дальнейшего полезно также ввести понятие “объединение” или равнодействующей двух материальных точек. Под этим мы будем понимать материальную точку, которая получится, если в центре тяжести двух материальных точек поместить массы обеих точек.

Пример. Пусть в концах невесомого тонкого стержня AB (рис. 2), длина которого равна 20 ед. Помещены такие массы: в A — 6 ед., в B — 2 ед. Центром тяжести материальных точек (A, 6) и (B, 2) будет точка C , лежащая на стержне AB , определяемая условием: 6CA=2CB , или CB=3CA . Поэтому АВ=CB+CA=4AC . Отсюда 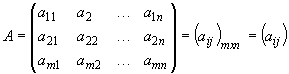(ед.). Объединение материальных точек (A, 6) и (B,2) будет материальная точка (С, 8) .

Центр тяжести трёх материальных точек находится следующим образом: находят объединение двух из этих материальных точек и затем ищут центр тяжести образовавшейся таким образом четвёртой материальной точки и третей из данных материальных точек.

Вообще, центр тяжести n материальных точек при n>2 находится так: надо сначала найти центр тяжести n-1 материальных точек, поместить в этой точке массы всех n-1 точек, затем найти центр тяжести этой вновь образовавшейся материальной точки с n -й материальной точкой.

Если поместить в центре тяжести несколько материальных точек массы всех этих точек, то образующуюся таким образом новую материальную точку назовём объединением данных материальных точек.

Для решения задач важны следующие простейшие свойства центров тяжести.

1. Положение центра тяжести n материальных точек не зависит от порядка, в котором последовательно объединяются эти точки. ( Теорема о единственности центра тяжести для системы из n материальных точек.)
2. Положение центра тяжести системы из n материальных точек не изменится, если заменить несколько материальных точек их объединением. ( Теорема о возможности группировки материальных точек.)

При рассмотрении некоторых вопросов механики оказывается выгодным ввести понятие статического момента.

Пусть имеется некоторая точка C и, кроме того, материальная точка A º (A, m) . Статическим моментом материальной точки А относительно точки С мы назовём произведение m × CA и будем его кратко обозначать так: Мом _С А .

Пользуясь понятием статического момента, определение центра тяжести можно сформулировать так: точка С называется центром тяжести двух материальных точек A º (A, m ₁ ) и B º (B, m ₂ ) , если С лежит на отрезке АВ и Мом _С А =Мом _С B.

Пусть теперь на некотором луче с началом S (рис. 3) расположена система из некоторых n материальных точек

Статическим моментом этой системы относительно начала луча S называют сумму моментов всех точек системы относительно начала луча,

т.е. сумму K= Мом _S A ₁ + Мом _S A ₂ + Мом _S A ₃ +…+ Мом _S A _n или, подробнее,

Пример. Если система состоит из трёх точек (A ₁ , 1), (A ₂ , 4), (A ₃ , 9) и SA ₁ =1, SA ₂ =2, SA ₃ =3 (рис. 4), то статический момент системы равен

Понятно, что в системе SGC момент будет иметь размерность г × см. Но мы ранее договорились, что размерность будем каждый раз подразумевать, но нигде не указывать.

В наших рассуждениях основными объектами были « материальные точки » . С точки зрения математики материальная точка — это комплекс, состоящий из геометрической точки и некоторого (положительного) числа.

В математике не раз приходится сталкиваться с таким явлением: комплекс из двух каких-то математических объектов рассматривают как некоторый новый объект, который затем уже подвергается специальному изучению. Так, например, в курсе алгебры вводится понятие комплексного числа как комплекса (пары) двух действительных чисел.

В строгих курсах геометрии таким образом вводится, например, понятие отрезка как комплекса (пары) двух точек; понятие угла может быть введено сходным образом: угол можно рассматривать как комплекс двух лучей с общим началом.

Если имеется у нас какая-либо материальная точка А º (A, m) , то мы (геометрическую) точку A будем иногда называть носителем или аффиксом этой материальной точки, а число m будем по-прежнему называть массой этой материальной точки.

Равенству вида (A, a) º (B, b) мы придаём такой смысл: две материальные точки имеют один и тот же носитель (A º B) и равные массы (a º b).

Решение почти всех ранее рассмотренных задач опиралось на то, что мы « объединяли некоторые материальные точки в их центре тяжести » ; точнее, заменяли некоторые материальные точки их объединением . При этом под объединением двух материальных точек (A, a) и (B, b) мы понимали некоторую новую материальную точку (С, a+b) , где С — центр тяжести двух данных материальных точек. Можно было бы так сказать: объединением двух материальных точек называется такая новая материальная точка, носителем которой является центр тяжести данных материальных точек и масса которых равна сумме масс этих материальных точек.

Вместо « объединения » можно употреблять выражение « сумма » .

Если материальная точка С º (С, с) является объединением двух других материальных точек A º (A, a) и B º (B, b) , то мы будем это записывать так:

(A, a) + (B, b) = (C, c)

или, короче,

A + B = C .

Мы не будем исключать и тот случай, когда две материальные точки имеют один и тот же носитель. В этом случае, естественно, будем считать носителем объединения их общий носитель. Таким образом, (А, а) + (А, b) = (A, a+b) .

У нас возникает своеобразное исчисление, своеобразная алгебра. В этой алгебре имеет место переместительный закон: A + B = B + A . Это следует из самого определения центра тяжести двух материальных точек. Имеет место также сочетательный закон:

(A ₁ + A ₂ ) + A ₃ = A ₁ + (A ₂ + A ₃ ),

или, иначе,

[(A ₁ , m ₁ ) + (A ₂ , m ₂ )] + (A ₃ , m ₃ ) = (A ₁ , m ₁ ) + [(A ₂ , m ₂ ) + (A ₃ , m ₃ )].

Подробнее: Найдём ли мы сначала объединение A ₁₂ двух материальных точек А ₁ и А ₂ и затем найдём объединение этой материальной точки А ₁₂ с третьей материальной точкой А ₃ , или сначала найдём объединение А ₂₃ материальных точек А ₂ и А ₃ , а затем найдём объединение материальных точек А ₁ и А ₂₃ , в обоих случаях мы придём к одному и тому же результату, к одной и той же материальной точке.

Понятно, что смысл этого утверждения состоит в том, что центр тяжести трёх материальных точек не зависит от порядка, в котором объединяются эти точки.

В наших рассуждениях « материальная точка » (A, m) выступала как комплекс, состоящий из некоторой геометрической точки А и некоторого положительного числа т . Это число т мы до сих пор называли массой . Однако его можно было бы назвать и каким-либо другим словом, скажем, « весом » . Все наши предыдущие рассуждения останутся, конечно, в силе, если заменить слово « масса » словом « вес » . Мы бы в таком случае уже не говорили, например, « рассмотрим материальную точку (А, т) с массой т » , а сказали бы: « рассмотрим материальную точку (А, т) с весом т » .

До сих пор мы наглядно представляли материальную точку (А, т) в виде материального шарика, размерами которого можно пренебречь, имеющего массу т . Но с таким же успехом мы могли бы наглядно представить ту же материальную точку в виде такого же шарика с весом т .

Мы далее рассматривали центр тяжести двух материальных точек вида (A, a) и (B, b) и определяли его по правилу рычага. Если мы хотим этот центр тяжести наглядно представить в виде центра тяжести двух шариков, помещённых в точках А и В и весящих соответственно а и b единиц, то нужно сделать несколько оговорок (которые, впрочем, само собой подразумеваются). Во всяком случае эти шарики должны быть на небольшом расстоянии друг от друга, настолько небольшом, чтобы можно было без чувствительной погрешности считать, что при свободном падении они будут перемещаться параллельно и с одним и тем же ускорением. Кроме того, если шарики из различных материалов, то важно, чтобы удельным весом газа или жидкости, заполняющей окружающую их среду, возможно было пренебречь. Такие условия практически будут соблюдены, например, если мы не выйдем за пределы, скажем, комнаты или даже города.

До сих пор, рассматривая материальную точку, то есть пару вида (А, т) ,мы всегда полагали, что её « масса » (или « вес » ) — положительное число. Для решения некоторых геометрических задач весьма полезно рассмотреть и такой случай, когда это число т может быть произвольным действительным числом . Такую пару мы, сохраняя старую терминологию, будем по-прежнему называть материальной точкой, а для числа т сохраним старое название « масса » (или « вес » ). Как же себе наглядно представить « материальную точку » с отрицательной « массой » ?

Приведём одну конкретную физическую картину, которая позволит читателю наглядно представить материальные точки с произвольными вещественными « массами » .

Пусть имеется какой-то бассейн, заполненный водой. Пусть шарик, который висит в воздухе (точнее, в пустоте) р единиц (скажем, р грамм), помещён в какую-то точку А внутри этого бассейна.

Рассмотрим сначала случай, когда удельный вес шарика больше 1 (например, когда шарик железный). Понятно, что шарик пойдёт в этом случае ко дну. Если под водой взвесить этот шарик (скажем, с помощью пружинных весов), то весы покажут меньше , чем р единиц. Нетрудно, если будет необходимость, узнать, сколько будет весить шарик под водой. Пусть удельный вес шарика равен d , а объём V . Тогда V=p/d. Считая удельный вес воды равным 1, найдём что вес воды в объёме, занимаемом шариком, равен (p/d) × 1=p/d . В силу закона Архимеда вес т шарика под водой (его « подводный вес » ) определяется по такой формуле:

(*)

Понятно, что т — подводный вес шарика — это результирующая сила, которая получается от сложения двух сил, действующих на шарик: силы тяжести и выталкивающей силы воды.

Обратим внимание на то, что в рассматриваемом случае (при d> 1) m >0 и эта сила направлена вниз . Пусть теперь удельный вес шарика меньше 1 (например, когда шарик сделан из пробки ). В этом случае шарик будет выталкиваться из воды ( « вверх » ). Результирующая сила m , под действием которой шарик будет выталкиваться вверх, будет в соответствии с законом Архимеда равна по-прежнему

,

но теперь это выражение отрицательно (ибо d <1) и, следовательно, сила направлена вверх .

Пусть, наконец, d =1, то есть удельный вес шарика равен удельному весу воды. Такой шарик можно себе представить изготовленным из дерева и содержащим металлическую сердцевину (причём металл и дерево должны, понятно, быть взяты во вполне определённом отношении). Можно его себе представить изготовленным также из специальной пластмассы. Его вес в воде по-прежнему определяется по (*), а так как d =1, то т =0, то есть такой шарик в воде невесом. При любом положении точки А в воде он останется в покое.

Таким образом, при любом d ( d> 0) выражение (*) характеризует величину результирующей силы, которая действует на шарик; она направлена « вниз » при т >0 (т.е. при d >1) и « вверх » при т <0 (т.е. при d <1). При т >0 мы эту силу назвали « подводным весом шарика » . То же название мы сохраним и при т £ 0. Таким образом, подводный вес шарика может выражаться как положительным, так и отрицательным числом или нулём.

Перейдём теперь к наглядному истолкованию « материальных точек » . Материальную точку (А, т) при любом т (положительном, отрицательном или равном нулю) мы можем наглядно представлять в виде шарика, размерами которого можно пренебречь, помещённого в точке А и имеющего подводный вес т .

Значит, то число т , которое мы условились называть « массой » материальной точки, мы истолковываем, как « подводный вес шарика » . При т >0 мы материальную точку (А, т) наглядно представляем в виде шарика, тонущего в воде (например, железного). При т <0 соответственно, всплывающего на поверхность воды (например, пробкового), а при т =0 — из пластмассы — с таким же удельным весом, что и у воды. В воде он будет невесомым. Будучи помещён в какой-либо точке, он под действием силы тяжести и выталкивающей силы воды останется на месте.

Если будет идти речь о двух материальных точках, то мы их можем себе наглядно представлять нанизанными на тонком прямолинейном стержне, изготовленном из той же « невесомой » (в воде) пластмассы, о которой мы говорили выше. Ниже мы будем говорить о центре тяжести двух материальных точек. Практически этот центр тяжести можно наглядно представить как точку, в которой нужно подпереть или за которую нужно подвесить невесомый (в воде) стержень для того, чтобы он вместе с нанизанными на нём « материальными точками » оказался в безразличном равновесии.

Всегда ли найдётся такая точка на этом стержне между этими двумя « материальными точками » ? Не может ли она оказаться вне отрезка, соединяющего данные материальные точки? Не может ли случиться, что такой точки вовсе нет? Это мы выясним ниже.

Аналогичным образом можно себе представить центр тяжести любого числа материальных точек.

Встречающееся ниже понятие « объединение нескольких материальных точек » можно наглядно истолковать как равнодействующую подводных весов всех тех шариков, которые наглядно изображают эти материальные точки.

Иногда полезно дать более широкое наглядное толкование понятия материальной точки с произвольной вещественной « массой » .

Сделаем одно предварительное замечание. На каждой прямой мы можем выбрать положительное направление и единицу масштаба. Если это уже сделано, то прямую иногда называют осью .

Каждый отрезок (скажем, АВ ) можно рассматривать как направленный, причём сначала мы называем начало отрезка ( А ), а затем — его конец ( В ); направление отрезка — от А к В . Если отрезок лежит на оси (или параллелен ей), то его направление может:

1. совпадать с направлением оси;
2. быть противоположным направлением оси.

В первом случае мы величиной отрезка называем его длину; во втором случае величиной отрезка мы называем его длину, взятую со знаком минус (-).

Таким образом, величина отрезка , лежащего на какой-нибудь оси, или параллельного оси — это его длина, взятая со знаком плюс или минус, в зависимости от того, будут ли направление отрезка и оси одинаковы или противоположны. Величину отрезка АВ будем обозначать так: АВ .

В нашем примере (рис. 5) АВ =3, DC = -2, ВА = -3. Вообще АВ = - ВА .

Вернёмся теперь к вопросу о возможном физическом истолковании материальных точек с произвольными вещественными массами.

Мы будем представлять, что в пространстве произвольным образом выбрана какая-либо ось l . Материальную точку (А, т) можно наглядно истолковать как силу, параллельную оси l и приложенную к точке А .

Число т ( « масса » ) характеризует абсолютную величину (или, как говорят иногда, « напряжение » ) и направление этой силы: сила и ось одинаково направлены, если т >0, и противоположно направлены, если т <0; по абсолютной величине сила равна ½ т ½ (единицам силы). Если т =0, то сила равна нулю. Материальную точку вида (А, 0) можно назвать « незагруженной точкой » или « нулевой силой » .

Когда будем ниже говорить о « центре тяжести нескольких материальных точек » , то его можно себе наглядно представлять как центр параллельных сил , а « объединение нескольких материальных точек » — как равнодействующую нескольких параллельных сил, приложенную в центре параллельных сил.

Для геометрических приложений важно, что почти всё основное, что мы говорили относительно материальных точек с положительными массами, возможно обобщить на случай материальных точек с произвольными вещественными массами.

Понятие центра тяжести двух материальных точек (с произвольными вещественными массами) можно ввести так.

Центром тяжести двух материальных точек (А, а) и (B, b) (рис. 6) называется такая точка С , лежащая на оси АВ (положительное направление от А к В ), которая удовлетворяет условию: а × АС =b × СВ .

Центр тяжести С двух материальных точек (А, а) и (B, b) будет лежать между А и В , лишь если « массы » а и b одного знака. Если а и b разных знаков, то С вне отрезка АВ (рис. 7).

Лишь в одном случае центр тяжести материальных точек (А, а) и (B, b) с различными носителями ( А ¹ В ) не существует, — именно, когда массы их противоположны по знаку, но не равны по абсолютной величине (то есть, если а = -b ¹ 0 ). В связи с этим мы будем называть две материальные точки вида (А, а) и (В, -а) ( А ¹ В , а ¹ 0 ) механической парой .

Этот случай можно себе представить как предельный для того случая, когда а ¹ -b , но а ® -b . Если а ¹ -b , а ¹ 0 , b ¹ 0 , то можно написать 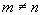, т.е. 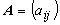. Если а ® -b , то а + b ® 0 и, следовательно, АС ® ¥ , то есть точка С неограниченно удаляется вдоль прямой АВ . Поэтому иногда говорят, что если a = -b , то центр тяжести двух материальных точек (А, а) и (B, b) « лежит в бесконечно удалённой точке прямой АВ » .

Оставаясь здесь в рамках элементарной геометрии, мы будем эту фразу рассматривать как образное выражение того, что центра тяжести в данном случае нет.

Если одна из двух материальных точек является незагруженной, а “масса” другой материальной точки отлична от нуля, то их центр тяжести совпадает с носителем загруженной точки. В связи с этим имеет смысл все незагруженные точки считать равными, то есть считать, что при любых А и В ( А, 0) º º (В, 0) .

Задача о нахождении центров тяжести двух незагруженных точек является неопределенной: существует бесконечно много точек, которые можно рассматривать в качестве центров тяжестей этих двух точек. Мы не будем останавливаться на рассмотрении этого случая.

 

 

Идея барицентрических координат.

Выберем на плоскости произвольный треугольник АВС (рис. 8), который в дальнейшем назовем координатным , или базисным треугольником Мебиуса. Пусть р ¹ 0 и (Р, р) ¾ произвольная материальная точка, лежащая в плоскости этого треугольника. Тогда возможно подобрать для точек А , В , С такие массы а , b , с (не обязательно положительные), чтобы объединением трех материальных точек (А, а) , (В, b) и (С, с) служила точка (Р, р) . Это можно себе представить следующим образом.

Ясно, что не может быть одновременно РА ½ ½ ВС, РВ ½ ½ СА, РС ½ ½ АВ . Пусть, для определённости, РА и ВС не параллельны. Соединим Р с А и отметим точку А ₁ , в которой АР встречает прямую ВС . Подберём три действительных числа а, b, c так, чтобы

b × BA ₁ = c × A ₁ C ,

a × AP = (b + c) × PA ₁ ,

a + b + c = p.

Это всегда возможно сделать. Тогда

(P, p) = (A, a) + (B, b) + (C, c).

Обратно, если возьмём три произвольных действительных числа a, b, c , причём a + b + c ¹ 0 , то существует вполне определённая материальная точка (Р, р) такая, что (Р, р) = (A, a) + (B, b) + (C, c).

Таким образом, каждую материальную точку Р º (Р, р) на плоскости можно вполне охарактеризовать тремя числами, а именно тремя массами a, b и с , которые надо поместить в вершинах базисного треугольника, чтобы точка Р оказалась объединением трёх образующихся при этом материальных точек (A, a), (B, b) и (C, c) . Эти три числа называют барицентрическими координатами материальной точки Р ( « барицентр » означает « центр тяжести » ): а — первая барицентрическая координата, b — вторая, с — третья. Понятно, что те же три числа a, b, c определяют также положение носителя материальной точки Р . Поэтому эти три числа называют также барицентрическими координатами (геометрической) точки Р .

Таким образом, выражение « барицентрическими координатами точки Р служат числа a, b, c » означает только то, что имеет место равенство

(A, a) + (B, b) + (C, c) = (P, p),

где

p = a + b + c.

Если массы трёх материальных точек увеличить (или уменьшить) в одно и то же число раз, то от этого положение их центра тяжести не изменится. Поэтому барицентрическими координатами геометрической точки Р будут также числа k × a, k × b, k × c, где k — любое действительное число, не равное нулю.

Итак, геометрическая точка Р (в отличие от материальной точки Р ) имеет бесконечно много троек барицентрических координат, причём каждая из этих троек может быть получена из какой-либо одной тройки ( a, b, c ) путём умножения на какую-либо константу k , отличную от нуля.

Если точка Р находится внутри координатного треугольника, то все три её барицентрические координаты одного знака (их можно считать положительными). Если точка Р — на какой-либо стороне координатного треугольника или на её продолжении, то хотя бы одна барицентрическая координата этой точки равна нулю. В остальных случаях две координаты точки Р — одного знака, а третья имеет противоположный знак.

Если точка Р расположена внутри базисного треугольника ABC , то в качестве её барицентрических координат можно принять площади треугольников BPC, CPA и APB .

Применение барицентрических координат позволяет внести одно существенное упрощение в рассуждения, связанное с рассмотрением материальных точек : рассмотрение любых произвольно расположенных материальных точек в любом числе сводится к рассмотрению только таких материальных точек, которые имеют носителями вершины базисного треугольника.